| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 8 Quadrilaterals
Welcome to this comprehensive resource providing detailed solutions for the NCERT Exemplar problems for Class 9 Mathematics, Chapter 8: Quadrilaterals. These Exemplar questions represent a significant step up from standard textbook exercises, demanding a much deeper understanding and application of geometric properties. The focus shifts decisively towards rigorous proofs, exploring the necessary and sufficient conditions for classifying quadrilaterals, and tackling complex applications, particularly involving the crucial Mid-point Theorem. Mastering this chapter requires strong deductive reasoning skills and the ability to construct logical arguments based on established geometric principles.
The solutions begin by reinforcing the fundamental Angle Sum Property of Quadrilaterals (sum of interior angles is $360^\circ$) but quickly delve into the specific properties of various types of quadrilaterals. A primary focus is on Parallelograms. The solutions demonstrate not just the application but often the proof of their defining properties:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- Consecutive angles are supplementary.
- Diagonals bisect each other.
Crucially, the solutions also cover the converse theorems – the conditions that are sufficient to prove a given quadrilateral is a parallelogram. For instance, proving that if one pair of opposite sides of a quadrilateral is both equal and parallel, then it is a parallelogram, or if the diagonals bisect each other, then it is a parallelogram. These conditions are frequently tested in Exemplar problems.
Building upon parallelograms, the properties of special parallelograms – Rectangles, Rhombuses, and Squares – are explored in detail. The solutions often show how their specific properties (like equal diagonals in a rectangle, perpendicular diagonals in a rhombus, or both in a square) can be proven, frequently relying on the principles of triangle congruence established in the previous chapter. Properties related to less common quadrilaterals like Kites and Trapeziums are also addressed as needed.
A major highlight and frequently tested concept in the Class 9 Exemplar for this chapter is the Mid-point Theorem and its Converse.
- Mid-point Theorem: The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
- Converse of Mid-point Theorem: The line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Exemplar problems demand a versatile application of these powerful theorems. The solutions demonstrate their use in intricate figures to prove lines are parallel, find unknown lengths, prove that certain points are mid-points, or establish properties of new quadrilaterals formed by joining the mid-points of the sides of other figures (e.g., proving that the quadrilateral formed by joining the mid-points of the sides of any quadrilateral is always a parallelogram). Successfully applying these theorems often requires careful identification of the relevant triangles within a complex diagram.
Addressing diverse question formats (MCQs, Fill-in-the-Blanks, True/False, Short/Long Answer), these solutions emphasize the construction of formal, well-structured proofs with precise geometric justifications for each step. They provide clearly annotated diagrams, logical application of theorems, and strategic approaches to solving complex problems. Engaging with this resource is essential for students aiming to master the geometry of quadrilaterals and develop the proficiency in geometric proof required for success in higher mathematics.
Sample Question 1 (Before Exercise 8.1)
Write the correct answer:
Sample Question 1: Diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90º and ∠BDC = 50º, then ∠OAB is
(A) 90º
(B) 50º
(C) 40º
(D) 10º
Answer:
Solution:
The correct option is (C) 40º.
Here is the step-by-step explanation:
Given:
ABCD is a parallelogram where diagonals AC and BD intersect at O.
$\angle BOC = 90^\circ$
$\angle BDC = 50^\circ$
To Find:
The measure of $\angle OAB$.
Solution:
In a parallelogram, opposite sides are parallel. So, AB || DC.
Considering AB || DC and BD as the transversal line intersecting them, the alternate interior angles are equal.
$\angle ABD = \angle BDC$
[Alternate Interior Angles]
Since it is given that $\angle BDC = 50^\circ$,
$\angle ABD = 50^\circ$
The angle $\angle ABD$ is the same as $\angle ABO$.
So, $\angle ABO = 50^\circ$.
Now, since AC is a straight line, the angles $\angle AOB$ and $\angle BOC$ form a linear pair.
$\angle AOB + \angle BOC = 180^\circ$
[Linear Pair]
Substituting the given value of $\angle BOC = 90^\circ$:
$\angle AOB + 90^\circ = 180^\circ$
$\angle AOB = 180^\circ - 90^\circ$
$\angle AOB = 90^\circ$
Now, consider the triangle $\triangle AOB$. The sum of all angles in a triangle is $180^\circ$.
$\angle OAB + \angle ABO + \angle AOB = 180^\circ$
[Angle Sum Property of a Triangle]
Substituting the values we found:
$\angle OAB + 50^\circ + 90^\circ = 180^\circ$
$\angle OAB + 140^\circ = 180^\circ$
$\angle OAB = 180^\circ - 140^\circ$
$\angle OAB = 40^\circ$
Thus, the measure of $\angle OAB$ is 40º.
Exercise 8.1
Write the correct answer in each of the following:
Question 1. Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is
(A) 90º
(B) 95º
(C) 105º
(D) 120º
Answer:
We know that the sum of the interior angles of a quadrilateral is $360^\circ$.
Let the three given angles be $\angle A = 75^\circ$, $\angle B = 90^\circ$, and $\angle C = 75^\circ$. Let the fourth angle be $\angle D$.
According to the property of quadrilaterals:
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
Substitute the given values into the equation:
$75^\circ + 90^\circ + 75^\circ + \angle D = 360^\circ$
Sum the known angles:
$(75^\circ + 75^\circ) + 90^\circ + \angle D = 360^\circ$
$150^\circ + 90^\circ + \angle D = 360^\circ$
$240^\circ + \angle D = 360^\circ$
Solve for $\angle D$:
$\angle D = 360^\circ - 240^\circ$
$\angle D = 120^\circ$
Thus, the fourth angle of the quadrilateral is $120^\circ$.
The correct option is (D) $120^\circ$.
Question 2. A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is
(A) 55º
(B) 50º
(C) 40º
(D) 25º
Answer:
Solution:
The correct option is (B) 50º.
Here is the step-by-step explanation:
Given:
A rectangle, let's call it ABCD.
A diagonal is inclined to one side of the rectangle at 25º. Let the diagonal be AC and the side be DC. So, $\angle ACD = 25^\circ$.
To Find:
The acute angle between the diagonals AC and BD.
Solution:
Let the diagonals AC and BD intersect at point O.
We know that the diagonals of a rectangle are equal in length and bisect each other. Therefore:
AC = BD
And, OA = OC = $\frac{1}{2}$AC, and OB = OD = $\frac{1}{2}$BD.
Since AC = BD, it follows that:
OA = OB = OC = OD
Now, consider the triangle $\triangle ODC$.
Since OC = OD (from the property of diagonals), $\triangle ODC$ is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are also equal.
$\angle ODC = \angle OCD$
[Angles opposite equal sides]
We are given that $\angle ACD = 25^\circ$, which is the same as $\angle OCD$.
So, $\angle OCD = 25^\circ$.
Therefore, $\angle ODC = 25^\circ$.
Now, using the angle sum property in $\triangle ODC$:
$\angle DOC + \angle ODC + \angle OCD = 180^\circ$
[Angle Sum Property of a Triangle]
Substituting the values of the angles:
$\angle DOC + 25^\circ + 25^\circ = 180^\circ$
$\angle DOC + 50^\circ = 180^\circ$
$\angle DOC = 180^\circ - 50^\circ$
$\angle DOC = 130^\circ$
The angles between the two diagonals are $\angle DOC$ and $\angle BOC$ (which form a linear pair).
$\angle DOC + \angle BOC = 180^\circ$
[Linear Pair]
$130^\circ + \angle BOC = 180^\circ$
$\angle BOC = 180^\circ - 130^\circ$
$\angle BOC = 50^\circ$
The two angles between the diagonals are $130^\circ$ (obtuse) and $50^\circ$ (acute).
The question asks for the acute angle between the diagonals, which is $50^\circ$.
Question 3. ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is
(A) 40º
(B) 45º
(C) 50º
(D) 60º
Answer:
Solution:
The correct option is (C) 50º.
Here is the step-by-step explanation:
Given:
ABCD is a rhombus.
$\angle ACB = 40^\circ$
To Find:
The measure of $\angle ADB$.
Solution:
In a rhombus, the opposite sides are parallel. Therefore, AD || BC.
Considering AD || BC and the diagonal AC as a transversal line, the alternate interior angles must be equal.
$\angle DAC = \angle ACB$
[Alternate Interior Angles]
Since we are given that $\angle ACB = 40^\circ$, we have:
$\angle DAC = 40^\circ$
We also know that the diagonals of a rhombus bisect each other at right angles (90º). Let the diagonals intersect at point O.
$\angle AOD = 90^\circ$
Now, let's consider the triangle $\triangle AOD$. The sum of the angles in a triangle is $180^\circ$.
$\angle DAO + \angle AOD + \angle ADO = 180^\circ$
[Angle Sum Property of a Triangle]
Substituting the values we know ($\angle DAO$ is the same as $\angle DAC$):
$40^\circ + 90^\circ + \angle ADO = 180^\circ$
$130^\circ + \angle ADO = 180^\circ$
$\angle ADO = 180^\circ - 130^\circ$
$\angle ADO = 50^\circ$
The angle $\angle ADO$ is the same as $\angle ADB$.
Therefore, $\angle ADB = 50^\circ$.
Alternate Solution:
In a rhombus, all sides are equal. In $\triangle BCD$, we have BC = CD.
Since the sides are equal, it is an isosceles triangle, but we don't know the base angles directly.
Let's use another property. The diagonals of a rhombus bisect the angles.
So, diagonal AC bisects $\angle BCD$. This means:
$\angle ACD = \angle ACB = 40^\circ$.
Therefore, the full angle $\angle BCD = \angle ACB + \angle ACD = 40^\circ + 40^\circ = 80^\circ$.
In a rhombus, adjacent angles are supplementary (add up to $180^\circ$).
$\angle ADC + \angle BCD = 180^\circ$
$\angle ADC + 80^\circ = 180^\circ$
$\angle ADC = 180^\circ - 80^\circ = 100^\circ$
The diagonal BD bisects $\angle ADC$.
Therefore, $\angle ADB = \frac{1}{2} \angle ADC$
$\angle ADB = \frac{1}{2} \times 100^\circ = 50^\circ$.
Question 4. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
(A) PQRS is a rectangle
(B) PQRS is a parallelogram
(C) diagonals of PQRS are perpendicular
(D) diagonals of PQRS are equal.
Answer:
Solution:
The correct option is (C) diagonals of PQRS are perpendicular.
Here is the step-by-step explanation:
Given:
A quadrilateral PQRS. Let A, B, C, and D be the mid-points of the sides PQ, QR, RS, and SP respectively. The quadrilateral ABCD formed by joining these mid-points in order is a rectangle.
To Find:
The condition that must be true for the quadrilateral PQRS.
Proof:
Let's use the Mid-point Theorem.
In $\triangle PQS$, A is the mid-point of PQ and D is the mid-point of SP.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
AD || QS and AD = $\frac{1}{2}$ QS
... (i)
Similarly, in $\triangle RQS$, B is the mid-point of QR and C is the mid-point of RS.
By the Mid-point Theorem:
BC || QS and BC = $\frac{1}{2}$ QS
... (ii)
From equations (i) and (ii), we can conclude that AD || BC and AD = BC. Since one pair of opposite sides is equal and parallel, ABCD is a parallelogram.
Now, let's consider the diagonal PR.
In $\triangle PQR$, A is the mid-point of PQ and B is the mid-point of QR.
By the Mid-point Theorem:
AB || PR and AB = $\frac{1}{2}$ PR
... (iii)
We are given that ABCD is a rectangle. A property of a rectangle is that its adjacent sides are perpendicular, which means one of its angles is $90^\circ$.
Let's consider the angle $\angle DAB = 90^\circ$.
From our findings:
AD || QS (from i)
AB || PR (from iii)
The angle between two lines is the same as the angle between any two lines parallel to them. Therefore, the angle between the sides AB and AD of the parallelogram ABCD is the same as the angle between the diagonals PR and QS of the quadrilateral PQRS.
Since ABCD is a rectangle, its adjacent sides are perpendicular.
AB $\perp$ AD
This implies that the lines parallel to AB and AD must also be perpendicular.
PR $\perp$ QS
Thus, for the quadrilateral ABCD to be a rectangle, the diagonals of the original quadrilateral PQRS must be perpendicular.
Question 5. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if
(A) PQRS is a rhombus
(B) PQRS is a parallelogram
(C) diagonals of PQRS are perpendicular
(D) diagonals of PQRS are equal.
Answer:
Solution:
The correct option is (D) diagonals of PQRS are equal.
Here is the step-by-step explanation:
Given:
A quadrilateral PQRS. Let A, B, C, and D be the mid-points of the sides PQ, QR, RS, and SP respectively. The quadrilateral ABCD formed by joining these mid-points in order is a rhombus.
To Find:
The condition that must be true for the quadrilateral PQRS.
Proof:
Let's use the Mid-point Theorem.
In $\triangle PQS$, A is the mid-point of PQ and D is the mid-point of SP.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
AD || QS and AD = $\frac{1}{2}$ QS
... (i)
Now, consider the diagonal PR.
In $\triangle PQR$, A is the mid-point of PQ and B is the mid-point of QR.
By the Mid-point Theorem:
AB || PR and AB = $\frac{1}{2}$ PR
... (ii)
We are given that the quadrilateral ABCD is a rhombus. A key property of a rhombus is that all its sides are equal in length.
Therefore, the adjacent sides of the rhombus ABCD must be equal.
AD = AB
Now, substituting the values from equations (i) and (ii):
$\frac{1}{2}$ QS = $\frac{1}{2}$ PR
Multiplying both sides by 2, we get:
QS = PR
This result shows that the lengths of the diagonals of the original quadrilateral PQRS must be equal.
Thus, for the quadrilateral formed by joining the mid-points to be a rhombus, the diagonals of the original quadrilateral must be equal.
Question 6. If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3 : 7 : 6 : 4, then ABCD is a
(A) rhombus
(B) parallelogram
(C) trapezium
(D) kite
Answer:
Solution:
The correct option is (C) trapezium.
Here is the step-by-step explanation:
Given:
A quadrilateral ABCD where the angles A, B, C, and D, taken in order, are in the ratio 3 : 7 : 6 : 4.
To Find:
The type of quadrilateral ABCD.
Solution:
We know that the sum of all interior angles of a quadrilateral is $360^\circ$.
Let the common ratio for the angles be $x$.
Then the angles are:
$\angle A = 3x$
$\angle B = 7x$
$\angle C = 6x$
$\angle D = 4x$
According to the angle sum property of a quadrilateral:
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
$3x + 7x + 6x + 4x = 360^\circ$
$20x = 360^\circ$
$x = \frac{360^\circ}{20}$
$x = 18^\circ$
Now, we can find the measure of each angle:
$\angle A = 3x = 3 \times 18^\circ = 54^\circ$
$\angle B = 7x = 7 \times 18^\circ = 126^\circ$
$\angle C = 6x = 6 \times 18^\circ = 108^\circ$
$\angle D = 4x = 4 \times 18^\circ = 72^\circ$
Now, let's check the properties of different quadrilaterals:
1. Parallelogram/Rhombus: In a parallelogram, opposite angles are equal. Here, $\angle A = 54^\circ$ and $\angle C = 108^\circ$, so $\angle A \neq \angle C$. Also, $\angle B = 126^\circ$ and $\angle D = 72^\circ$, so $\angle B \neq \angle D$. Since opposite angles are not equal, ABCD is not a parallelogram or a rhombus.
2. Kite: In a kite, one pair of opposite angles is equal. Here, no pair of opposite angles is equal. So, it is not a kite.
3. Trapezium: In a trapezium, one pair of opposite sides is parallel. If two lines are parallel, then the sum of the consecutive interior angles on the same side of a transversal is $180^\circ$.
Let's check the sum of adjacent angles:
$\angle A + \angle B = 54^\circ + 126^\circ = 180^\circ$
$\angle C + \angle D = 108^\circ + 72^\circ = 180^\circ$
Since the sum of consecutive interior angles $\angle A$ and $\angle B$ is $180^\circ$, this implies that the sides AD and BC are parallel (AD || BC), with AB acting as a transversal. Similarly, since $\angle C + \angle D = 180^\circ$, AD || BC with CD as a transversal.
Let's also check the other pair of consecutive angles:
$\angle A + \angle D = 54^\circ + 72^\circ = 126^\circ \neq 180^\circ$. So, AB is not parallel to DC.
Since ABCD has exactly one pair of parallel sides (AD || BC), it is a trapezium.
Question 7. If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a
(A) rectangle
(B) rhombus
(C) parallelogram
(D) quadrilateral whose opposite angles are supplementary
Answer:
Solution:
The correct option is (D) quadrilateral whose opposite angles are supplementary.
Here is the step-by-step explanation:
Given:
A quadrilateral ABCD.
The bisectors of ∠A and ∠B intersect at P.
The bisectors of ∠B and ∠C intersect at Q.
The bisectors of ∠C and ∠D intersect at R.
The bisectors of ∠D and ∠A intersect at S.
To Find:
The properties of the quadrilateral PQRS.
Solution:
Let's consider the triangle $\triangle ADS$.
AS is the bisector of $\angle A$, so $\angle DAS = \frac{1}{2}\angle A$.
DS is the bisector of $\angle D$, so $\angle ADS = \frac{1}{2}\angle D$.
The sum of angles in a triangle is $180^\circ$.
In $\triangle ADS$:
$\angle ASD + \angle DAS + \angle ADS = 180^\circ$
$\angle ASD + \frac{1}{2}\angle A + \frac{1}{2}\angle D = 180^\circ$
$\angle ASD = 180^\circ - \frac{1}{2}(\angle A + \angle D)$
The angle $\angle PSR$ of the quadrilateral PQRS is vertically opposite to $\angle ASD$.
$\angle PSR = \angle ASD = 180^\circ - \frac{1}{2}(\angle A + \angle D)$
... (i)
Similarly, let's consider the triangle $\triangle BQC$.
BQ is the bisector of $\angle B$, so $\angle CBQ = \frac{1}{2}\angle B$.
CQ is the bisector of $\angle C$, so $\angle BCQ = \frac{1}{2}\angle C$.
In $\triangle BQC$:
$\angle BQC + \angle CBQ + \angle BCQ = 180^\circ$
$\angle BQC + \frac{1}{2}\angle B + \frac{1}{2}\angle C = 180^\circ$
$\angle BQC = 180^\circ - \frac{1}{2}(\angle B + \angle C)$
The angle $\angle PQR$ of the quadrilateral PQRS is vertically opposite to $\angle BQC$.
$\angle PQR = \angle BQC = 180^\circ - \frac{1}{2}(\angle B + \angle C)$
... (ii)
Now, let's find the sum of the opposite angles $\angle PSR$ and $\angle PQR$ of the quadrilateral PQRS by adding equations (i) and (ii).
$\angle PSR + \angle PQR = \left[180^\circ - \frac{1}{2}(\angle A + \angle D)\right] + \left[180^\circ - \frac{1}{2}(\angle B + \angle C)\right]$
$\angle PSR + \angle PQR = 360^\circ - \frac{1}{2}(\angle A + \angle B + \angle C + \angle D)$
We know that the sum of all angles in the quadrilateral ABCD is $360^\circ$.
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
Substituting this value:
$\angle PSR + \angle PQR = 360^\circ - \frac{1}{2}(360^\circ)$
$\angle PSR + \angle PQR = 360^\circ - 180^\circ$
$\angle PSR + \angle PQR = 180^\circ$
Since the sum of one pair of opposite angles of the quadrilateral PQRS is $180^\circ$, the sum of the other pair of opposite angles must also be $180^\circ$.
This proves that PQRS is a quadrilateral whose opposite angles are supplementary.
Question 8. If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form
(A) a square
(B) a rhombus
(C) a rectangle
(D) any other parallelogram
Answer:
Solution:
The correct option is (C) a rectangle.
Here is the step-by-step explanation:
Given:
Two parallel lines APB and CQD are intersected by a transversal line PQ.
To Find:
The type of quadrilateral formed by the bisectors of the angles ∠APQ, ∠BPQ, ∠CQP and ∠PQD.
Solution:
Let the bisectors of the four interior angles form a quadrilateral. Let's analyze the properties of this quadrilateral.
1. Relationship between bisectors of a linear pair:
The angles ∠APQ and ∠BPQ form a linear pair on the line APB.
$\angle APQ + \angle BPQ = 180^\circ$
[Linear Pair]
Let PR be the bisector of $\angle APQ$ and PS be the bisector of $\angle BPQ$. The angle between these two bisectors is:
$\angle RPS = \angle RPQ + \angle SPQ = \frac{1}{2}\angle APQ + \frac{1}{2}\angle BPQ$
$\angle RPS = \frac{1}{2}(\angle APQ + \angle BPQ) = \frac{1}{2}(180^\circ) = 90^\circ$
This means the angle formed at one vertex of the quadrilateral is 90º.
2. Relationship between bisectors of consecutive interior angles:
Since APB || CQD, the consecutive interior angles are supplementary.
$\angle APQ + \angle CQP = 180^\circ$
Let the bisector of $\angle APQ$ and the bisector of $\angle CQP$ intersect at a point M.
In the triangle formed, $\triangle PQM$, we have:
$\angle MPQ = \frac{1}{2}\angle APQ$
$\angle MQP = \frac{1}{2}\angle CQP$
By the angle sum property of a triangle:
$\angle PMQ = 180^\circ - (\angle MPQ + \angle MQP)$
$\angle PMQ = 180^\circ - \left(\frac{1}{2}\angle APQ + \frac{1}{2}\angle CQP\right)$
$\angle PMQ = 180^\circ - \frac{1}{2}(\angle APQ + \angle CQP)$
$\angle PMQ = 180^\circ - \frac{1}{2}(180^\circ) = 180^\circ - 90^\circ = 90^\circ$
This proves that one of the interior angles of the quadrilateral formed by the bisectors is 90º.
3. Relationship between bisectors of alternate interior angles:
Since APB || CQD, the alternate interior angles are equal.
$\angle APQ = \angle PQD$
The bisector of $\angle APQ$ makes an angle of $\frac{1}{2}\angle APQ$ with the transversal PQ. The bisector of $\angle PQD$ makes an angle of $\frac{1}{2}\angle PQD$ with the transversal PQ.
Since $\angle APQ = \angle PQD$, their halves are also equal. These equal angles are alternate interior angles for the two bisector lines. Therefore, the bisector of $\angle APQ$ is parallel to the bisector of $\angle PQD$.
Similarly, $\angle BPQ = \angle CQP$ (alternate interior angles). Their bisectors will also be parallel to each other.
Conclusion:
From point (3), we see that the quadrilateral formed has two pairs of parallel opposite sides. Therefore, the quadrilateral is a parallelogram.
From points (1) or (2), we see that one of the interior angles of this parallelogram is 90º.
A parallelogram with one right angle is a rectangle.
Hence, the quadrilateral formed by the bisectors is a rectangle.
Question 9. The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is
(A) a rhombus
(B) a rectangle
(C) a square
(D) any parallelogram
Answer:
Solution:
The correct option is (B) a rectangle.
Here is the step-by-step explanation:
Given:
A rhombus PQRS. Let A, B, C, and D be the mid-points of the sides PQ, QR, RS, and SP respectively.
To Find:
The type of quadrilateral formed by joining the mid-points A, B, C, and D in order.
Solution:
Let's use the Mid-point Theorem to determine the properties of the quadrilateral ABCD.
1. Proving ABCD is a Parallelogram:
In $\triangle PQS$, A is the mid-point of PQ and D is the mid-point of SP.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
AD || QS and AD = $\frac{1}{2}$ QS
... (i)
Similarly, in $\triangle RQS$, B is the mid-point of QR and C is the mid-point of RS.
By the Mid-point Theorem:
BC || QS and BC = $\frac{1}{2}$ QS
... (ii)
From (i) and (ii), we have AD || BC and AD = BC. Since one pair of opposite sides is equal and parallel, ABCD is a parallelogram.
2. Finding the Angles of Parallelogram ABCD:
Now consider the other diagonal PR. In $\triangle PQR$, A and B are mid-points of PQ and QR.
By the Mid-point Theorem:
AB || PR
... (iii)
We know from (i) that AD || QS and from (iii) that AB || PR.
The angle between the adjacent sides AB and AD of the parallelogram will be the same as the angle between the lines they are parallel to, which are the diagonals PR and QS of the rhombus.
A key property of a rhombus is that its diagonals are perpendicular to each other.
So, PR $\perp$ QS, which means the angle between them is $90^\circ$.
Therefore, the angle between AB and AD is also $90^\circ$.
Since ABCD is a parallelogram with one angle equal to $90^\circ$, it must be a rectangle.
Note: The figure will be a square only if the diagonals of the rhombus are equal (PR = QS). If the diagonals are equal, the rhombus is a square. In that specific case, the mid-point figure is also a square. But for a general rhombus, the figure is a rectangle.
Question 10. D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
(A) a square
(B) a rectangle
(C) a rhombus
(D) a parallelogram
Answer:
Solution:
The correct option is (D) a parallelogram.
Here is the step-by-step explanation:
Given:
In $\triangle ABC$:
- D is the mid-point of side AB.
- E is the mid-point of side AC.
- O is any point on side BC.
- P is the mid-point of OB.
- Q is the mid-point of OC.
To Find:
The type of quadrilateral DEQP.
Solution:
We will use the Mid-point Theorem, which states that the line segment connecting the mid-points of two sides of a triangle is parallel to the third side and is half the length of the third side.
Step 1: Analyze $\triangle ABO$
In $\triangle ABO$, D is the mid-point of AB and P is the mid-point of OB.
By the Mid-point Theorem:
DP || AO and DP = $\frac{1}{2}$ AO
... (i)
Step 2: Analyze $\triangle ACO$
In $\triangle ACO$, E is the mid-point of AC and Q is the mid-point of OC.
By the Mid-point Theorem:
EQ || AO and EQ = $\frac{1}{2}$ AO
... (ii)
Step 3: Compare DP and EQ
From equations (i) and (ii), we can see that:
DP || AO and EQ || AO $\implies$ DP || EQ
DP = $\frac{1}{2}$ AO and EQ = $\frac{1}{2}$ AO $\implies$ DP = EQ
Step 4: Conclusion
In the quadrilateral DEQP, we have found that one pair of opposite sides (DP and EQ) is both equal and parallel.
A quadrilateral is a parallelogram if one pair of its opposite sides is equal and parallel.
Therefore, DEQP is a parallelogram.
Verification with the other pair of sides:
In $\triangle ABC$, D is the mid-point of AB and E is the mid-point of AC.
By the Mid-point Theorem: DE || BC and DE = $\frac{1}{2}$ BC.
Now consider the side PQ. P and Q are mid-points of OB and OC respectively.
PQ = PO + OQ = $\frac{1}{2}$ OB + $\frac{1}{2}$ OC = $\frac{1}{2}$ (OB + OC)
Since O is a point on the line segment BC, OB + OC = BC.
So, PQ = $\frac{1}{2}$ BC.
This shows that DE = PQ. Also, since DE || BC and the segment PQ lies on the line BC, we have DE || PQ.
Since both pairs of opposite sides are parallel and equal, DEQP is confirmed to be a parallelogram.
Question 11. The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if,
(A) ABCD is a rhombus
(B) diagonals of ABCD are equal
(C) diagonals of ABCD are equal and perpendicular
(D) diagonals of ABCD are perpendicular.
Answer:
Solution:
The correct option is (C) diagonals of ABCD are equal and perpendicular.
Here is the step-by-step explanation:
Given:
A quadrilateral ABCD. Let P, Q, R, and S be the mid-points of the sides AB, BC, CD, and DA respectively. The quadrilateral PQRS formed by joining these mid-points in order is a square.
To Find:
The condition that must be true for the quadrilateral ABCD.
Solution:
We will use the Mid-point Theorem to analyze the properties of the quadrilateral PQRS.
In $\triangle ABC$, P and Q are the mid-points of AB and BC respectively.
By the Mid-point Theorem:
PQ || AC and PQ = $\frac{1}{2}$ AC
... (i)
In $\triangle ADC$, S and R are the mid-points of AD and CD respectively.
By the Mid-point Theorem:
SR || AC and SR = $\frac{1}{2}$ AC
... (ii)
From (i) and (ii), we get PQ || SR and PQ = SR. This proves that PQRS is a parallelogram.
Similarly, by considering $\triangle ABD$ and $\triangle BCD$, we find:
PS || BD and PS = $\frac{1}{2}$ BD
... (iii)
Now, we are given that PQRS is a square. A square has two key properties:
1. All angles are $90^\circ$ (which means it's a rectangle).
2. All sides are equal (which means it's a rhombus).
Let's apply these properties.
Condition for PQRS to be a Rectangle (Angle property):
For PQRS to be a rectangle, its adjacent sides must be perpendicular. Let's take PQ $\perp$ PS.
From (i), we have PQ || AC.
From (iii), we have PS || BD.
If PQ $\perp$ PS, then the lines they are parallel to must also be perpendicular. Therefore:
AC $\perp$ BD
This means the diagonals of the original quadrilateral ABCD must be perpendicular.
Condition for PQRS to be a Rhombus (Side property):
For PQRS to be a rhombus, its adjacent sides must be equal. Let's take PQ = PS.
From (i), we have PQ = $\frac{1}{2}$ AC.
From (iii), we have PS = $\frac{1}{2}$ BD.
If PQ = PS, then:
$\frac{1}{2}$ AC = $\frac{1}{2}$ BD
AC = BD
This means the diagonals of the original quadrilateral ABCD must be equal in length.
Conclusion for PQRS to be a Square:
Since a square is both a rectangle and a rhombus, both conditions derived above must be satisfied simultaneously.
Therefore, for PQRS to be a square, the diagonals of ABCD must be equal and perpendicular.
Question 12. The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32º and ∠AOB = 70º, then ∠DBC is equal to
(A) 24º
(B) 86º
(C) 38º
(D) 32º
Answer:
Solution:
The correct option is (C) 38º.
Here is the step-by-step explanation:
Given:
ABCD is a parallelogram.
Diagonals AC and BD intersect at point O.
$\angle DAC = 32^\circ$
$\angle AOB = 70^\circ$
To Find:
The measure of $\angle DBC$.
Solution:
Since ABCD is a parallelogram, its opposite sides are parallel. Therefore, AD || BC.
Considering AD || BC and the diagonal BD as a transversal, the alternate interior angles are equal.
$\angle DBC = \angle BDA$
[Alternate Interior Angles] ... (i)
Our goal is to find $\angle BDA$. We can do this by analyzing the triangle $\triangle AOD$.
The diagonal BD is a straight line. The angles $\angle AOB$ and $\angle AOD$ form a linear pair on the line BD.
$\angle AOD + \angle AOB = 180^\circ$
[Linear Pair]
Substituting the given value of $\angle AOB = 70^\circ$:
$\angle AOD + 70^\circ = 180^\circ$
$\angle AOD = 180^\circ - 70^\circ = 110^\circ$
Now, consider the triangle $\triangle AOD$. The sum of its angles is $180^\circ$.
$\angle OAD + \angle AOD + \angle ADO = 180^\circ$
[Angle Sum Property of a Triangle]
We know that $\angle OAD$ is the same as $\angle DAC$, which is given as $32^\circ$. And we found $\angle AOD = 110^\circ$. $\angle ADO$ is the same as $\angle BDA$.
Substituting these values:
$32^\circ + 110^\circ + \angle BDA = 180^\circ$
$142^\circ + \angle BDA = 180^\circ$
$\angle BDA = 180^\circ - 142^\circ = 38^\circ$
From equation (i), we know that $\angle DBC = \angle BDA$.
Therefore, $\angle DBC = 38^\circ$.
Alternate Solution:
Since AD || BC and the diagonal AC is a transversal, the alternate interior angles are equal.
$\angle BCA = \angle DAC = 32^\circ$
[Alternate Interior Angles]
The angles $\angle AOB$ and $\angle BOC$ form a linear pair on the straight line AC.
$\angle BOC + \angle AOB = 180^\circ$
[Linear Pair]
$\angle BOC + 70^\circ = 180^\circ$
$\angle BOC = 180^\circ - 70^\circ = 110^\circ$
Now, consider the triangle $\triangle BOC$. The sum of its angles is $180^\circ$.
$\angle OBC + \angle BCO + \angle BOC = 180^\circ$
[Angle Sum Property of a Triangle]
Substituting the values we know ($\angle BCO = \angle BCA$ and $\angle OBC = \angle DBC$):
$\angle DBC + 32^\circ + 110^\circ = 180^\circ$
$\angle DBC + 142^\circ = 180^\circ$
$\angle DBC = 180^\circ - 142^\circ = 38^\circ$
Question 13. Which of the following is not true for a parallelogram?
(A) opposite sides are equal
(B) opposite angles are equal
(C) opposite angles are bisected by the diagonals
(D) diagonals bisect each other.
Answer:
Solution:
The correct option is (C) opposite angles are bisected by the diagonals.
Here is an explanation for each option:
(A) opposite sides are equal
This is a fundamental property of a parallelogram. By definition, a parallelogram is a quadrilateral with two pairs of parallel sides, and a consequence of this is that the opposite sides are equal in length. So, this statement is true.
(B) opposite angles are equal
This is another fundamental property of a parallelogram. The opposite angles of any parallelogram are always equal in measure. So, this statement is true.
(C) opposite angles are bisected by the diagonals
This statement is not always true for a general parallelogram. The diagonals bisect the angles only in the special cases of a rhombus and a square. In a parallelogram that is not a rhombus (for example, a rectangle that is not a square, or a slanted parallelogram), the diagonals do not bisect the opposite angles.
As shown in the figure of a general parallelogram, the diagonal AC divides $\angle DAB$ into two angles, $\angle DAC$ and $\angle CAB$, which are not equal. Therefore, this statement is false for a general parallelogram.
(D) diagonals bisect each other
This is a defining property of a parallelogram. The two diagonals of any parallelogram intersect at their midpoints, meaning they bisect each other. So, this statement is true.
Conclusion:
The only statement that is not true for all parallelograms is that the opposite angles are bisected by the diagonals.
Question 14. D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is
(A) ∠DAE = ∠EFC
(B) AE = EF
(C) DE = EF
(D) ∠ADE = ∠ECF.
Answer:
Solution:
The correct option is (C) DE = EF.
Here is the step-by-step explanation:
Given:
- In $\triangle ABC$, D is the mid-point of AB and E is the mid-point of AC.
- DE is produced to a point F.
To Prove:
CF is equal and parallel to DA (i.e., CF = DA and CF || DA).
Required:
The additional information needed for the proof.
Solution:
To prove that CF = DA and CF || DA, a common strategy is to prove that the triangles involving these sides are congruent. Let's consider $\triangle ADE$ and $\triangle CFE$.
In $\triangle ADE$ and $\triangle CFE$, we have:
AE = CE
[Given that E is the mid-point of AC]
$\angle AED = \angle CEF$
[Vertically opposite angles]
Now we have a side and an angle (Side-Angle) for both triangles. To prove congruence using the SAS (Side-Angle-Side) rule, we need the sides adjacent to the equal angles to be equal. This means we need the additional information that:
DE = EF
If we assume this condition (DE = EF) is true, let's see if we can complete the proof:
In $\triangle ADE$ and $\triangle CFE$:
1. AE = CE (E is the mid-point of AC)
2. $\angle AED = \angle CEF$ (Vertically opposite angles)
3. DE = EF (Required additional information from option C)
By SAS congruence criterion, we have:
$\triangle ADE \cong \triangle CFE$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent):
DA = FC
... (i)
$\angle DAE = \angle FCE$
... (ii)
From (i), we have proved that CF is equal to DA.
From (ii), the angles $\angle DAE$ and $\angle FCE$ are alternate interior angles formed by the lines DA (which is part of AB) and FC, with AC as the transversal. Since these alternate interior angles are equal, the lines must be parallel.
So, DA || FC.
Thus, with the additional information DE = EF, we can prove that CF is equal and parallel to DA. This corresponds to forming a parallelogram ADCF because its diagonals AC and DF bisect each other at E.
Sample Question 1 to 4 (Before Exercise 8.2)
Sample Question 1: ABCD is a parallelogram. If its diagonals are equal, then find the value of ∠ABC.
Answer:
Given:
A parallelogram ABCD.
The diagonals are equal, i.e., AC = BD.
To Find:
The value of $\angle ABC$.
Solution:
To find the value of $\angle ABC$, we will prove that two adjacent triangles formed by the diagonals are congruent.
Consider $\triangle ABC$ and $\triangle DCB$.
AB = DC
(Opposite sides of a parallelogram are equal)
BC = CB
(Common side)
AC = DB
(Given that diagonals are equal)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle ABC \cong \triangle DCB$
By CPCTC (Corresponding parts of congruent triangles are congruent), we have:
$\angle ABC = \angle DCB$
... (i)
We know that in a parallelogram, the adjacent angles are supplementary (their sum is $180^\circ$). The sides AB and DC are parallel, and BC is a transversal.
$\angle ABC + \angle DCB = 180^\circ$
[Consecutive interior angles are supplementary]
From equation (i), we can substitute $\angle DCB$ with $\angle ABC$:
$\angle ABC + \angle ABC = 180^\circ$
$2\angle ABC = 180^\circ$
$\angle ABC = \frac{180^\circ}{2}$
$\angle ABC = 90^\circ$
Thus, the value of $\angle ABC$ is 90°.
Alternate Solution:
We know a key property of quadrilaterals: A parallelogram with equal diagonals is a rectangle.
Since ABCD is a parallelogram with equal diagonals, it must be a rectangle.
By definition, all interior angles of a rectangle are right angles ($90^\circ$).
Therefore, $\angle ABC = 90^\circ$.
Sample Question 2: Diagonals of a rhombus are equal and perpendicular to each other. Is this statement true? Give reason for your answer.
Answer:
The statement is false.
Reason:
The given statement makes two claims about the diagonals of a rhombus:
1. They are perpendicular to each other.
2. They are equal to each other.
For the entire statement to be true, both claims must be correct.
Claim 1: Diagonals of a rhombus are perpendicular to each other.
This part of the statement is true. It is a fundamental property of a rhombus that its diagonals always bisect each other at right angles ($90^\circ$).
Claim 2: Diagonals of a rhombus are equal to each other.
This part of the statement is false. The diagonals of a rhombus are not necessarily equal. They are only equal in the special case where the rhombus is a square. In a general (non-square) rhombus, one diagonal is longer than the other.
Since a statement connected by "and" requires both parts to be true, and the claim that the diagonals are equal is false for a general rhombus, the entire statement is false.
Sample Question 3: Three angles of a quadrilateral ABCD are equal. Is it a parallelogram? Why or why not?
Answer:
No, a quadrilateral with three equal angles is not necessarily a parallelogram.
Reason:
For a quadrilateral to be a parallelogram, both pairs of its opposite angles must be equal. Let's analyze the situation where three angles are equal.
Let the three equal angles of a quadrilateral ABCD be $x$.
Let $\angle A = \angle B = \angle C = x$.
We know that the sum of all angles in a quadrilateral is $360^\circ$.
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
$x + x + x + \angle D = 360^\circ$
$3x + \angle D = 360^\circ$
$\angle D = 360^\circ - 3x$
Now, for ABCD to be a parallelogram, the opposite angles must be equal.
1. $\angle A = \angle C$ (This is already true since both are $x$).
2. $\angle B = \angle D$ (This must also be true).
For the second condition to hold, we must have:
$x = 360^\circ - 3x$
$4x = 360^\circ$
$x = 90^\circ$
This shows that the quadrilateral is a parallelogram only in the specific case where the three equal angles are $90^\circ$. If $x = 90^\circ$, then the fourth angle is also $\angle D = 360^\circ - 3(90^\circ) = 90^\circ$. A quadrilateral with all four angles equal to $90^\circ$ is a rectangle, which is a type of parallelogram.
However, if the three equal angles are not $90^\circ$, the quadrilateral is not a parallelogram.
Counterexample:
Let the three equal angles of a quadrilateral ABCD be $100^\circ$.
So, $\angle A = 100^\circ$, $\angle B = 100^\circ$, and $\angle C = 100^\circ$.
The fourth angle, $\angle D$, would be:
$\angle D = 360^\circ - (100^\circ + 100^\circ + 100^\circ) = 360^\circ - 300^\circ = 60^\circ$.
Now, let's check the opposite angles of this quadrilateral:
- $\angle A = 100^\circ$ and $\angle C = 100^\circ$. (These are equal).
- $\angle B = 100^\circ$ and $\angle D = 60^\circ$. (These are not equal).
Since one pair of opposite angles ($\angle B$ and $\angle D$) is unequal, the quadrilateral is not a parallelogram.
Therefore, a quadrilateral with three equal angles is not always a parallelogram.
Sample Question 4: Diagonals AC and BD of a quadrilateral ABCD intersect each other at O such that OA : OC = 3: 2. Is ABCD a parallelogram? Why or why not?
Answer:
No, ABCD is not a parallelogram.
Reason:
One of the fundamental properties and a sufficient condition for a quadrilateral to be a parallelogram is that its diagonals must bisect each other.
This means that the point of intersection of the diagonals must be the midpoint of each diagonal.
In the given quadrilateral ABCD, the diagonals AC and BD intersect at point O.
If ABCD were a parallelogram, then O would have to be the midpoint of AC. This would imply that the lengths of the segments OA and OC are equal.
If OA = OC, then the ratio of their lengths would be:
$\frac{OA}{OC} = 1$
This means the ratio OA : OC must be 1 : 1.
However, we are given that the ratio is:
OA : OC = 3 : 2
Since the ratio 3 : 2 is not equal to 1 : 1, we can conclude that OA $\neq$ OC. This means the diagonal AC is not bisected by the diagonal BD.
Because the diagonals do not bisect each other, the quadrilateral ABCD cannot be a parallelogram.
Exercise 8.2
Question 1. Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
Answer:
Given:
A parallelogram ABCD where diagonals AC and BD intersect at point O.
OA = 3 cm
OD = 2 cm
To Find:
The lengths of the diagonals AC and BD.
Solution:
We know that a fundamental property of a parallelogram is that its diagonals bisect each other. This means that the point of intersection of the diagonals is the midpoint of each diagonal.
Since the diagonals AC and BD intersect at O, O is the midpoint of both AC and BD.
For diagonal AC:
Since O is the midpoint of AC, the length of AC is twice the length of OA.
$AC = 2 \times OA$
Substituting the given value of OA = 3 cm:
$AC = 2 \times 3 \text{ cm} = 6 \text{ cm}$
For diagonal BD:
Similarly, since O is the midpoint of BD, the length of BD is twice the length of OD.
$BD = 2 \times OD$
Substituting the given value of OD = 2 cm:
$BD = 2 \times 2 \text{ cm} = 4 \text{ cm}$
Therefore, the lengths of the diagonals are AC = 6 cm and BD = 4 cm.
Question 2. Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.
Answer:
The statement is false.
Reason:
The diagonals of a parallelogram are not always perpendicular to each other. This property is only true for special types of parallelograms.
A parallelogram is a quadrilateral with two pairs of parallel sides. This includes rectangles, rhombuses, and squares.
-
In a general parallelogram (one that is not a rectangle or a rhombus), the diagonals bisect each other but are not perpendicular.
-
In a rectangle, the diagonals are equal and bisect each other, but they are not perpendicular (unless the rectangle is also a square).
-
In a rhombus, the diagonals bisect each other and are perpendicular. This is a defining property of a rhombus.
Since the statement claims this property is true for "a parallelogram" in general, it is considered false because it does not hold true for all cases (like a rectangle or a slanted parallelogram).
The property of having perpendicular diagonals is specific to a rhombus and a square (which is a special type of rhombus).
Question 3. Can the angles 110º, 80º, 70º and 95º be the angles of a quadrilateral? Why or why not?
Answer:
No, the angles $110^\circ, 80^\circ, 70^\circ$ and $95^\circ$ cannot be the angles of a quadrilateral.
Reason:
According to the angle sum property of a quadrilateral, the sum of all four interior angles must be exactly $360^\circ$.
Let's calculate the sum of the given angles:
$110^\circ + 80^\circ + 70^\circ + 95^\circ = 355^\circ$
The sum of the given angles is $355^\circ$.
Since this sum is not equal to $360^\circ$, these angles cannot form the interior angles of a quadrilateral.
Question 4. In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Answer:
The special name that can be given to this quadrilateral is a trapezium.
Reason:
We are given a quadrilateral ABCD where the sum of two adjacent angles, $\angle A$ and $\angle D$, is $180^\circ$.
Let's consider the sides AB and DC as two lines and the side AD as a transversal that intersects them.
The angles $\angle A$ (or $\angle DAB$) and $\angle D$ (or $\angle ADC$) are consecutive interior angles (or co-interior angles) on the same side of the transversal AD.
We know a key property of parallel lines: If a transversal intersects two lines such that the sum of the consecutive interior angles is $180^\circ$, then the two lines are parallel to each other.
Since we are given that:
$\angle A + \angle D = 180^\circ$
We can conclude that the lines AB and DC are parallel.
AB || DC
A quadrilateral which has at least one pair of parallel opposite sides is called a trapezium.
Therefore, the quadrilateral ABCD is a trapezium.
Question 5. All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
Answer:
The special name given to this quadrilateral is a rectangle.
Reason:
Let the quadrilateral be ABCD and let each of its equal angles be $x$.
So, we have $\angle A = \angle B = \angle C = \angle D = x$.
According to the angle sum property of a quadrilateral, the sum of all four interior angles is always $360^\circ$.
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
Substituting the value of each angle with $x$:
$x + x + x + x = 360^\circ$
$4x = 360^\circ$
$x = \frac{360^\circ}{4}$
$x = 90^\circ$
This shows that each angle of the quadrilateral is a right angle ($90^\circ$).
By definition, a quadrilateral in which all four angles are right angles is called a rectangle.
Note: A square also has all angles equal to $90^\circ$, but it must also have all sides equal. Since we are only given information about the angles, the most general and correct name for the quadrilateral is a rectangle.
Question 6. Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
Answer:
The statement is false.
Reason:
The given statement makes two claims about the diagonals of a rectangle:
- They are equal.
- They are perpendicular.
For the entire statement to be true, both claims must be correct.
Claim 1: Diagonals of a rectangle are equal.
This part of the statement is true. It is a fundamental property of all rectangles that their diagonals are equal in length.
Claim 2: Diagonals of a rectangle are perpendicular.
This part of the statement is false. The diagonals of a rectangle are not perpendicular unless the rectangle is also a square. In a general, non-square rectangle, the diagonals bisect each other but do not intersect at a right angle ($90^\circ$).
The property of having perpendicular diagonals belongs to a rhombus. Since a square is both a rectangle and a rhombus, its diagonals are both equal and perpendicular. However, the statement must hold for all rectangles to be considered true.
Since the second part of the "and" statement is false, the entire statement is false.
Question 7. Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.
Answer:
No, all four angles of a quadrilateral cannot be obtuse angles.
Reason:
An obtuse angle is an angle that measures more than $90^\circ$ but less than $180^\circ$.
The sum of the interior angles of any quadrilateral is always $360^\circ$.
Let the four angles of the quadrilateral be $\angle A$, $\angle B$, $\angle C$, and $\angle D$. If all four angles were obtuse, then each angle would be greater than $90^\circ$.
$\angle A > 90^\circ$
$\angle B > 90^\circ$
$\angle C > 90^\circ$
$\angle D > 90^\circ$
Summing these inequalities:
$\angle A + \angle B + \angle C + \angle D > 90^\circ + 90^\circ + 90^\circ + 90^\circ$
$\angle A + \angle B + \angle C + \angle D > 360^\circ$
This result shows that if all four angles were obtuse, their sum would be greater than $360^\circ$. However, the sum of the interior angles of a quadrilateral must be exactly $360^\circ$.
Since the calculated sum is greater than the required sum, it is impossible for a quadrilateral to have four obtuse angles.
Question 8. In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
Answer:
Given:
In a triangle $\triangle ABC$:
- AB = 5 cm
- BC = 8 cm
- CA = 7 cm
- D is the mid-point of side AB.
- E is the mid-point of side BC.
To Find:
The length of the line segment DE.
Solution:
We will use the Mid-point Theorem to solve this problem.
The Mid-point Theorem states that the line segment connecting the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of the length of the third side.
In $\triangle ABC$, we are given that D and E are the mid-points of sides AB and BC, respectively.
According to the Mid-point Theorem, the line segment DE will be parallel to the third side AC, and its length will be half the length of AC.
$DE = \frac{1}{2} AC$
(By Mid-point Theorem)
We are given the length of the side CA (which is the same as AC).
$AC = 7 \text{ cm}$
(Given)
Now, we substitute this value into the equation from the theorem:
$DE = \frac{1}{2} \times 7 \text{ cm}$
$DE = 3.5 \text{ cm}$
Therefore, the length of DE is 3.5 cm.
(Note: The lengths of AB and BC are extra information and are not required to determine the length of DE.)
Question 9. In Fig.8.1, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
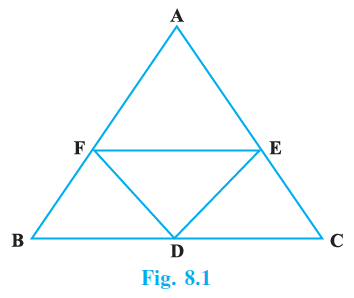
Answer:
Yes, we can say that $BD = CD$.
Reason:
We are given that BDEF and FDCE are parallelograms. A fundamental property of a parallelogram is that its opposite sides are equal in length.
1. For Parallelogram BDEF:
The side BD is opposite to the side FE.
Therefore, their lengths must be equal.
$BD = FE$
[Opposite sides of a parallelogram are equal] ... (i)
2. For Parallelogram FDCE:
The side CD is opposite to the side FE.
Therefore, their lengths must be equal.
$CD = FE$
[Opposite sides of a parallelogram are equal] ... (ii)
3. Conclusion:
From equation (i), we have $BD = FE$.
From equation (ii), we have $CD = FE$.
Since both BD and CD are equal to the same segment FE, they must be equal to each other.
Therefore, by comparing equations (i) and (ii), we can conclude that:
$BD = CD$
This also implies that D is the mid-point of the side BC.
Question 10. In Fig.8.2, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.
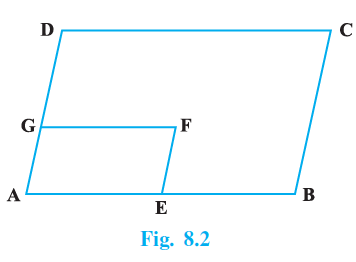
Answer:
Given:
ABCD is a parallelogram.
AEFG is a parallelogram.
$\angle C = 55^\circ$
To Determine:
The measure of $\angle F$.
Solution:
We are given that ABCD is a parallelogram. In a parallelogram, opposite angles are equal.
$\angle A = \angle C$
(Opposite angles of parallelogram ABCD)
Given $\angle C = 55^\circ$, so
$\angle A = 55^\circ$
We are also given that AEFG is a parallelogram. In parallelogram AEFG, the angle at vertex A is $\angle GAE$, which is the same angle $\angle A$ we found from parallelogram ABCD. In parallelogram AEFG, opposite angles are equal. The angle opposite to $\angle A$ (or $\angle GAE$) is $\angle F$.
$\angle F = \angle A$
(Opposite angles of parallelogram AEFG)
Since we determined that $\angle A = 55^\circ$:
$\angle F = 55^\circ$
Therefore, the measure of $\angle F$ is $55^\circ$.
Question 11. Can all the angles of a quadrilateral be acute angles? Give reason for your answer.
Answer:
No, all the angles of a quadrilateral cannot be acute angles.
Reason:
An acute angle is an angle whose measure is less than $90^\circ$.
The angle sum property of a quadrilateral states that the sum of all its four interior angles is always exactly $360^\circ$.
Let's assume that it is possible for a quadrilateral to have all four angles as acute angles. Let the four angles be $\angle A, \angle B, \angle C,$ and $\angle D$.
According to our assumption:
$\angle A < 90^\circ$
$\angle B < 90^\circ$
$\angle C < 90^\circ$
$\angle D < 90^\circ$
If we add these four inequalities, we get:
$\angle A + \angle B + \angle C + \angle D < 90^\circ + 90^\circ + 90^\circ + 90^\circ$
$\angle A + \angle B + \angle C + \angle D < 360^\circ$
This result shows that the sum of the four angles would be less than $360^\circ$. However, this contradicts the angle sum property of a quadrilateral, which states that the sum must be exactly $360^\circ$.
Therefore, our initial assumption is incorrect, and it is impossible for all four angles of a quadrilateral to be acute angles.
Question 12. Can all the angles of a quadrilateral be right angles? Give reason for your answer.
Answer:
Yes, all the angles of a quadrilateral can be right angles.
Reason:
A right angle is an angle that measures exactly $90^\circ$.
The sum of the interior angles of any quadrilateral is always equal to $360^\circ$.
Let the four angles of the quadrilateral be $\angle A$, $\angle B$, $\angle C$, and $\angle D$. If all four angles were right angles, then each angle would be $90^\circ$.
$\angle A = 90^\circ$
$\angle B = 90^\circ$
$\angle C = 90^\circ$
$\angle D = 90^\circ$
Let's find the sum of these angles:
Sum = $\angle A + \angle B + \angle C + \angle D$
Sum = $90^\circ + 90^\circ + 90^\circ + 90^\circ$
Sum = $4 \times 90^\circ$
Sum = $360^\circ$
Since the sum of the four angles is exactly equal to $360^\circ$, it is possible for a quadrilateral to have all four angles as right angles.
A quadrilateral with all four angles equal to $90^\circ$ is called a rectangle. A square is a special type of rectangle where all sides are also equal.
Question 13. Diagonals of a quadrilateral ABCD bisect each other. If ∠A = 35º, determine ∠B.
Answer:
Given:
A quadrilateral ABCD where the diagonals bisect each other.
$\angle A = 35^\circ$
To Find:
The measure of $\angle B$.
Solution:
We are given that the diagonals of the quadrilateral ABCD bisect each other.
A key property of quadrilaterals states that if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Therefore, ABCD is a parallelogram.
Another important property of a parallelogram is that its adjacent (or consecutive) angles are supplementary, which means their sum is $180^\circ$.
In parallelogram ABCD, $\angle A$ and $\angle B$ are adjacent angles.
$\angle A + \angle B = 180^\circ$
(Adjacent angles of a parallelogram are supplementary)
Substituting the given value of $\angle A = 35^\circ$ into the equation:
$35^\circ + \angle B = 180^\circ$
$\angle B = 180^\circ - 35^\circ$
$\angle B = 145^\circ$
Therefore, the measure of $\angle B$ is $145^\circ$.
Question 14. Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
Answer:
Given:
A quadrilateral ABCD in which opposite angles are equal.
So, $\angle A = \angle C$ and $\angle B = \angle D$.
Also, the length of side AB is given as 4 cm.
To Find:
The length of the side CD.
Solution:
We know a key theorem of quadrilaterals which states: If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Since we are given that the opposite angles of quadrilateral ABCD are equal, we can conclude that ABCD is a parallelogram.
Now, we use another fundamental property of a parallelogram: The opposite sides of a parallelogram are equal in length.
In the parallelogram ABCD, the side CD is opposite to the side AB.
Therefore, their lengths must be equal.
CD = AB
(Opposite sides of a parallelogram are equal)
We are given that AB = 4 cm.
Substituting this value, we get:
CD = 4 cm
Therefore, the length of CD is 4 cm.
Sample Question 1 to 3 (Before Exercise 8.3)
Sample Question 1: Angles of a quadrilateral are in the ratio 3 : 4 : 4 : 7. Find all the angles of the quadrilateral.
Answer:
Given:
The angles of a quadrilateral are in the ratio $3 : 4 : 4 : 7$.
To Find:
All the angles of the quadrilateral.
Solution:
Let the angles of the quadrilateral be $3x$, $4x$, $4x$, and $7x$, where $x$ is a common multiplier.
The sum of the interior angles of a quadrilateral is $360^\circ$.
Set up an equation based on the sum of the angles:
$(3x) + (4x) + (4x) + (7x) = 360^\circ$
Combine the terms with $x$:
$(3 + 4 + 4 + 7)x = 360^\circ$
18x = $360^\circ$
Solve for $x$:
x = $\frac{360^\circ}{18}$
x = $20^\circ$
Now, calculate the measure of each angle using the value of $x$:
First angle = $3x = 3 \times 20^\circ = 60^\circ$
Second angle = $4x = 4 \times 20^\circ = 80^\circ$
Third angle = $4x = 4 \times 20^\circ = 80^\circ$
Fourth angle = $7x = 7 \times 20^\circ = 140^\circ$
Let's check if the sum of these angles is $360^\circ$: $60^\circ + 80^\circ + 80^\circ + 140^\circ \ $$ = 140^\circ + 80^\circ + 140^\circ = 220^\circ + 140^\circ = 360^\circ$. The sum is correct.
The angles of the quadrilateral are $60^\circ$, $80^\circ$, $80^\circ$, and $140^\circ$.
Sample Question 2: In Fig.8.3, X and Y are respectively the mid-points of the opposite sides AD and BC of a parallelogram ABCD. Also, BX and DY intersect AC at P and Q, respectively. Show that AP = PQ = QC.
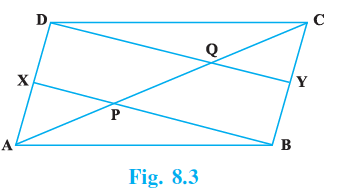
Answer:
Given:
A parallelogram ABCD.
X is the mid-point of the side AD.
Y is the mid-point of the side BC.
The lines BX and DY intersect the diagonal AC at points P and Q respectively.
To Prove:
AP = PQ = QC.
Proof:
Since ABCD is a parallelogram, its opposite sides are equal and parallel.
$AD = BC \text{ and } AD \ || \ BC$
(Properties of a parallelogram)
Multiplying the equality by $\frac{1}{2}$ on both sides:
$\frac{1}{2} AD = \frac{1}{2} BC$
We are given that X and Y are the mid-points of AD and BC, respectively.
So, $DX = \frac{1}{2} AD$ and $BY = \frac{1}{2} BC$.
Therefore, we can conclude that:
$DX = BY$
... (i)
Also, since AD || BC, their parts are also parallel.
$DX \ || \ BY$
... (ii)
Now, consider the quadrilateral XBYD. From (i) and (ii), we have one pair of opposite sides (DX and BY) that are equal and parallel.
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Thus, XBYD is a parallelogram.
Since XBYD is a parallelogram, its other pair of opposite sides must also be parallel.
$DY \ || \ BX$
This implies that DQ || XP and QY || PB.
Now, let's use the converse of the Mid-point Theorem.
In $\triangle ADQ$:
- X is the mid-point of the side AD. (Given)
- XP is parallel to DQ (since BX || DY).
By the converse of the Mid-point Theorem (which states that a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side), the line XP must bisect the side AQ.
Therefore, P is the mid-point of AQ.
$AP = PQ$
... (iii)
In $\triangle CPB$:
- Y is the mid-point of the side CB. (Given)
- YQ is parallel to PB (since DY || BX).
By the converse of the Mid-point Theorem, the line YQ must bisect the side CP.
Therefore, Q is the mid-point of CP.
$PQ = QC$
... (iv)
Conclusion:
From equation (iii), we have AP = PQ.
From equation (iv), we have PQ = QC.
Combining these two results, we get:
AP = PQ = QC
This shows that the points P and Q trisect the diagonal AC.
Hence Proved.
Sample Question 3: In Fig.8.4, AX and CY are respectively the bisectors of the opposite angles A and C of a parallelogram ABCD.
Show that AX || CY.
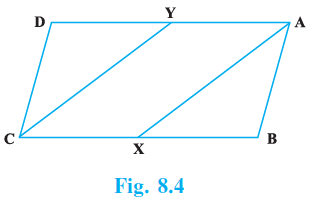
Answer:
Given:
A parallelogram ABCD in which AX is the bisector of $\angle A$ and CY is the bisector of $\angle C$.
X lies on side BC and Y lies on side AD.
To Prove:
AX || CY.
Proof:
Since ABCD is a parallelogram, its opposite angles are equal.
$\angle A = \angle C$
(Opposite angles of a parallelogram)
Multiplying both sides by $\frac{1}{2}$:
$\frac{1}{2}\angle A = \frac{1}{2}\angle C$
Since AX is the bisector of $\angle A$ and CY is the bisector of $\angle C$, we have:
$\angle BAX = \frac{1}{2}\angle A$ and $\angle DCY = \frac{1}{2}\angle C$
Therefore, we can conclude that:
$\angle BAX = \angle DCY$
... (i)
Now, let us consider the triangles $\triangle ABX$ and $\triangle CDY$.
In a parallelogram, opposite sides are equal and opposite angles are equal.
AB = CD
(Opposite sides of a parallelogram)
$\angle B = \angle D$
(Opposite angles of a parallelogram)
Now, in $\triangle ABX$ and $\triangle CDY$:
$\angle B = \angle D$
(Proved above)
AB = CD
(Proved above)
$\angle BAX = \angle DCY$
[From (i)]
Therefore, by ASA (Angle-Side-Angle) congruence criterion:
$\triangle ABX \cong \triangle CDY$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
BX = DY
... (ii)
We also know that the opposite sides of parallelogram ABCD are equal and parallel.
AD = BC and AD || BC
Subtracting equation (ii) from the equality $AD = BC$ is not straightforward. Let's reconsider. We need to prove AXCY is a parallelogram.
Since AD || BC, and Y is a point on AD and X is a point on BC, it follows that their parts are also parallel.
AY || XC
This is one pair of opposite sides of quadrilateral AXCY being parallel. If we can prove they are equal as well, then AXCY will be a parallelogram.
We know AD = BC. And from (ii) we have DY = BX.
AY = AD - DY
XC = BC - BX
Since AD = BC and DY = BX, their differences must be equal.
AY = XC
Now, in quadrilateral AXCY, we have one pair of opposite sides (AY and XC) which are both equal and parallel.
A quadrilateral is a parallelogram if one pair of its opposite sides is equal and parallel.
Therefore, AXCY is a parallelogram.
Since AXCY is a parallelogram, its other pair of opposite sides must also be parallel.
AX || CY
Hence Proved.
Exercise 8.3
Question 1. One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
Answer:
Given:
One angle of a quadrilateral is $108^\circ$.
The remaining three angles are equal.
To Find:
The measure of each of the three equal angles.
Solution:
Let the measure of each of the three equal angles be $x$.
The sum of the interior angles of a quadrilateral is $360^\circ$.
Set up an equation for the sum of the angles:
Sum of angles = $108^\circ + x + x + x$
Sum of angles = $108^\circ + 3x$
Equate the sum of the angles to $360^\circ$:
$108^\circ + 3x = 360^\circ$
(Sum of angles in a quadrilateral)
Subtract $108^\circ$ from both sides of the equation:
3x = $360^\circ - 108^\circ$
3x = $252^\circ$
Divide by 3 to find the value of $x$:
x = $\frac{252^\circ}{3}$
x = $84^\circ$
Thus, each of the three equal angles is $84^\circ$.
The three equal angles are $84^\circ$, $84^\circ$, and $84^\circ$.
Question 2. ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
Answer:
Given:
A trapezium ABCD in which AB || DC.
$\angle A = 45^\circ$
$\angle B = 45^\circ$
To Find:
The measures of angles C and D.
Solution:
In a trapezium, the sum of the consecutive interior angles between the parallel sides is $180^\circ$.
We are given that AB || DC.
To find $\angle D$:
Consider the parallel lines AB and DC and the transversal line AD.
The angles $\angle A$ and $\angle D$ are consecutive interior angles.
$\angle A + \angle D = 180^\circ$
(Sum of consecutive interior angles is $180^\circ$)
Substituting the given value of $\angle A = 45^\circ$:
$45^\circ + \angle D = 180^\circ$
$\angle D = 180^\circ - 45^\circ$
$\angle D = 135^\circ$
To find $\angle C$:
Now, consider the parallel lines AB and DC and the transversal line BC.
The angles $\angle B$ and $\angle C$ are consecutive interior angles.
$\angle B + \angle C = 180^\circ$
(Sum of consecutive interior angles is $180^\circ$)
Substituting the given value of $\angle B = 45^\circ$:
$45^\circ + \angle C = 180^\circ$
$\angle C = 180^\circ - 45^\circ$
$\angle C = 135^\circ$
Therefore, the measures of the angles are $\angle C = 135^\circ$ and $\angle D = 135^\circ$.
(Note: Since the base angles $\angle A$ and $\angle B$ are equal, this trapezium is an isosceles trapezium, and as a result, the other pair of base angles, $\angle C$ and $\angle D$, are also equal.)
Question 3. The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
Answer:
Given:
A parallelogram where the angle between two altitudes, drawn with reference to the vertex of an obtuse angle, is $60^\circ$.
To Find:
The angles of the parallelogram.
Solution:
Let ABCD be a parallelogram. Let $\angle B$ be an obtuse angle of the parallelogram. The phrase "altitudes ... through the vertex of an obtuse angle" is interpreted as the altitudes drawn from another vertex (here, D) to the two sides that form the obtuse angle (AB and BC).
Let's draw an altitude from vertex D to the extension of side AB, meeting at point N. So, DN $\perp$ AB.
Let's draw another altitude from vertex D to the extension of side BC, meeting at point M. So, DM $\perp$ BC.
We are given that the angle between these two altitudes is $60^\circ$.
$\angle NDM = 60^\circ$
Now, consider the quadrilateral NBMD.
The sum of the interior angles of a quadrilateral is $360^\circ$.
$\angle NBM + \angle BMD + \angle MDN + \angle DNB = 360^\circ$
By construction, we know:
$\angle BMD = 90^\circ$
$\angle DNB = 90^\circ$
And it is given that $\angle MDN = 60^\circ$.
Substituting these values into the sum of angles equation:
$\angle NBM + 90^\circ + 60^\circ + 90^\circ = 360^\circ$
$\angle NBM + 240^\circ = 360^\circ$
$\angle NBM = 360^\circ - 240^\circ$
$\angle NBM = 120^\circ$
The angle $\angle NBM$ is vertically opposite to the interior angle $\angle ABC$ of the parallelogram.
$\angle ABC = \angle NBM = 120^\circ$
(Vertically opposite angles)
So, the obtuse angle of the parallelogram is $120^\circ$.
In a parallelogram, adjacent angles are supplementary (add up to $180^\circ$). Let's find the adjacent acute angle, $\angle A$.
$\angle A + \angle B = 180^\circ$
$\angle A + 120^\circ = 180^\circ$
$\angle A = 180^\circ - 120^\circ = 60^\circ$
The acute angle of the parallelogram is $60^\circ$.
Since opposite angles of a parallelogram are equal:
$\angle C = \angle A = 60^\circ$
$\angle D = \angle B = 120^\circ$
Therefore, the angles of the parallelogram are $60^\circ, 120^\circ, 60^\circ,$ and $120^\circ$.
Question 4. ABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.
Answer:
Given:
A rhombus ABCD.
An altitude from vertex D to the side AB bisects AB. Let the foot of the altitude be M. So, DM $\perp$ AB and M is the mid-point of AB.
To Find:
The angles of the rhombus ABCD (i.e., $\angle A, \angle B, \angle C,$ and $\angle D$).
Solution:
Let M be the point on AB such that DM is the altitude from D to AB.
According to the given information:
1. DM $\perp$ AB, which means $\angle DMA = \angle DMB = 90^\circ$.
2. M is the mid-point of AB, which means AM = MB.
Now, let's consider the triangles $\triangle ADM$ and $\triangle BDM$.
AM = BM
(Given, M is the mid-point of AB)
$\angle DMA = \angle DMB$
(Each is $90^\circ$)
DM = DM
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle ADM \cong \triangle BDM$
By CPCTC (Corresponding parts of congruent triangles are equal), we have:
AD = BD
... (i)
We know that ABCD is a rhombus, and in a rhombus, all sides are equal in length.
AD = AB
(Sides of a rhombus) ... (ii)
From equations (i) and (ii), we can conclude:
AD = AB = BD
This means that the triangle $\triangle ABD$ is an equilateral triangle.
In an equilateral triangle, all interior angles are equal to $60^\circ$.
Therefore, $\angle A = 60^\circ$.
Now we can find the other angles of the rhombus using its properties:
1. Opposite angles are equal:
$\angle C = \angle A = 60^\circ$
2. Adjacent angles are supplementary (sum is $180^\circ$):
$\angle A + \angle B = 180^\circ$
$60^\circ + \angle B = 180^\circ$
$\angle B = 180^\circ - 60^\circ = 120^\circ$
3. Opposite angles are equal:
$\angle D = \angle B = 120^\circ$
Thus, the angles of the rhombus are $60^\circ, 120^\circ, 60^\circ,$ and $120^\circ$.
Question 5. E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram.
Answer:
Given:
A parallelogram ABCD.
E and F are points on the diagonal AC such that AE = CF.
To Prove:
The quadrilateral BFDE is a parallelogram.
Proof:
Let the diagonals of the parallelogram ABCD, which are AC and BD, intersect each other at point O.
Since the diagonals of a parallelogram bisect each other, O is the midpoint of both AC and BD.
OA = OC
... (i)
OB = OD
... (ii)
We are given that:
AE = CF
... (iii)
Now, subtracting equation (iii) from equation (i):
$OA - AE = OC - CF$
From the figure, we can see that the segment left after subtracting AE from OA is OE. Similarly, the segment left after subtracting CF from OC is OF.
So, we have:
OE = OF
... (iv)
Equation (iv) shows that O is the midpoint of the line segment EF.
From equation (ii), we already know that O is the midpoint of the line segment BD.
Now, let's consider the quadrilateral BFDE. Its diagonals are BD and EF.
Since the midpoint of diagonal BD and the midpoint of diagonal EF is the same point O, the diagonals of the quadrilateral BFDE bisect each other.
A quadrilateral is a parallelogram if its diagonals bisect each other.
Therefore, BFDE is a parallelogram.
Hence Proved.
Question 6. E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
Answer:
Given:
A trapezium ABCD in which AB || DC.
E is the mid-point of the side AD.
A line through E is drawn parallel to AB and intersects BC at F. So, EF || AB.
To Prove:
F is the mid-point of BC.
Construction:
Join the diagonal AC, which intersects the line segment EF at a point G.
Proof:
We are given that AB || DC and EF || AB.
Since two lines parallel to the same line are parallel to each other, we can conclude that all three lines are parallel:
AB || EF || DC.
Now, we will use the Converse of the Mid-point Theorem. This theorem states that a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Step 1: In triangle $\triangle ADC$
- E is the mid-point of the side AD. (Given)
- The line segment EG is a part of EF, and since EF || DC, we have EG || DC.
By applying the Converse of the Mid-point Theorem to $\triangle ADC$, the line EG must bisect the third side, AC.
Therefore, G is the mid-point of AC.
AG = GC
... (i)
Step 2: In triangle $\triangle ABC$
- G is the mid-point of the side AC. (Proved in Step 1)
- The line segment GF is a part of EF, and since EF || AB, we have GF || AB.
By applying the Converse of the Mid-point Theorem to $\triangle ABC$, the line GF must bisect the third side, BC.
Therefore, F is the mid-point of BC.
Hence Proved.
Question 7. Through A, B and C, lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ∆ ABC as shown in Fig.8.5. Show that BC = $\frac{1}{2}$ QR.
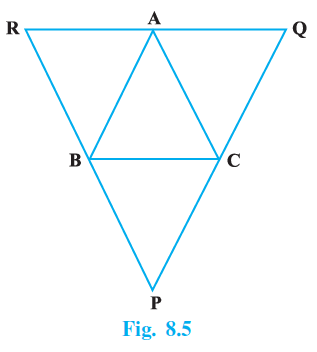
Answer:
Given:
In $\triangle ABC$:
- A line RQ is drawn through A parallel to BC (RQ || BC).
- A line PR is drawn through B parallel to AC (PR || AC).
- A line QP is drawn through C parallel to AB (QP || AB).
These lines form a larger triangle $\triangle PQR$.
To Prove:
$BC = \frac{1}{2} QR$.
Proof:
We will show that the vertices A, B, and C are the mid-points of the sides of $\triangle PQR$ by proving that certain quadrilaterals are parallelograms.
Step 1: Prove that ABCR is a parallelogram.
We are given the following parallel lines:
AR || BC
(Part of line RQ)
BR || AC
(Part of line PR)
Since both pairs of opposite sides are parallel, the quadrilateral ABCR is a parallelogram.
A property of a parallelogram is that its opposite sides are equal.
BC = AR
... (i)
Step 2: Prove that ABCQ is a parallelogram.
We are given the following parallel lines:
AQ || BC
(Part of line RQ)
CQ || AB
(Part of line QP)
Since both pairs of opposite sides are parallel, the quadrilateral ABCQ is a parallelogram.
Therefore, its opposite sides are equal.
BC = AQ
... (ii)
Step 3: Combine the results.
From equation (i), we have BC = AR.
From equation (ii), we have BC = AQ.
Combining these two, we get:
AR = AQ = BC
Since AR = AQ, it means that A is the mid-point of the side QR.
The total length of the side QR is:
$QR = AR + AQ$
Since AR = BC and AQ = BC, we can substitute these into the equation:
$QR = BC + BC$
$QR = 2 \times BC$
Rearranging this equation to make BC the subject:
$BC = \frac{1}{2} QR$
Hence Proved.
Question 8. D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆ DEF is also an equilateral triangle.
Answer:
Given:
An equilateral triangle $\triangle ABC$.
D, E, and F are the mid-points of sides BC, CA, and AB, respectively.
The mid-points are joined to form a smaller triangle, $\triangle DEF$.
To Prove:
$\triangle DEF$ is an equilateral triangle.
Proof:
Since $\triangle ABC$ is an equilateral triangle, all its sides are equal in length.
AB = BC = CA
... (i)
Now, we will use the Mid-point Theorem. The theorem states that the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half the length of the third side.
Let's apply this theorem to the sides of $\triangle DEF$.
1. For side DE:
D is the mid-point of BC and E is the mid-point of CA.
According to the Mid-point Theorem:
$DE = \frac{1}{2} AB$
... (ii)
2. For side EF:
E is the mid-point of CA and F is the mid-point of AB.
According to the Mid-point Theorem:
$EF = \frac{1}{2} BC$
... (iii)
3. For side FD:
F is the mid-point of AB and D is the mid-point of BC.
According to the Mid-point Theorem:
$FD = \frac{1}{2} CA$
... (iv)
From our given information in equation (i), we know that AB = BC = CA.
If we multiply this entire equality by $\frac{1}{2}$, we get:
$\frac{1}{2} AB = \frac{1}{2} BC = \frac{1}{2} CA$
Now, we can substitute the expressions from equations (ii), (iii), and (iv) into this equality:
DE = EF = FD
Since all three sides of $\triangle DEF$ are equal in length, it is an equilateral triangle.
Hence Proved.
Question 9. Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (Fig. 8.6). Show that AC and PQ bisect each other.

Answer:
Given:
A parallelogram ABCD.
P is a point on the side AB and Q is a point on the opposite side CD.
AP = CQ.
To Prove:
The line segments AC and PQ bisect each other.
Proof:
To prove that AC and PQ bisect each other, we will first prove that the quadrilateral APCQ is a parallelogram. If APCQ is a parallelogram, then its diagonals (AC and PQ) will bisect each other.
Since ABCD is a parallelogram, its opposite sides are parallel.
AB || DC
(Opposite sides of a parallelogram)
Since P is a point on AB and Q is a point on DC, the parts of these lines are also parallel.
AP || CQ
... (i)
We are also given that the lengths of these segments are equal.
AP = CQ
(Given) ... (ii)
Now, consider the quadrilateral APCQ. From equations (i) and (ii), we see that one pair of opposite sides (AP and CQ) is both parallel and equal.
A quadrilateral is a parallelogram if one pair of its opposite sides is equal and parallel.
Therefore, APCQ is a parallelogram.
We know that the diagonals of a parallelogram bisect each other.
Since AC and PQ are the diagonals of the parallelogram APCQ, they must bisect each other.
Hence Proved.
Alternate Solution:
Let the line segments AC and PQ intersect at a point O.
We can prove that AC and PQ bisect each other by showing that $\triangle AOP \cong \triangle COQ$.
In $\triangle AOP$ and $\triangle COQ$:
AP = CQ
(Given)
Since ABCD is a parallelogram, AB || DC. Considering AC as a transversal:
$\angle PAO = \angle QCO$
(Alternate interior angles)
Considering PQ as a transversal:
$\angle APO = \angle CQO$
(Alternate interior angles)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle AOP \cong \triangle COQ$
By CPCTC (Corresponding parts of congruent triangles are congruent):
OA = OC
OP = OQ
OA = OC means that O is the midpoint of AC.
OP = OQ means that O is the midpoint of PQ.
Since O is the midpoint of both line segments, we can conclude that AC and PQ bisect each other.
Hence Proved.
Question 10. In Fig. 8.7, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.
Answer:
Given:
A parallelogram ABCD.
P is the mid-point of the side BC. So, $BP = PC = \frac{1}{2}BC$.
The line segment AP bisects $\angle A$. So, $\angle BAP = \angle DAP$.
To Prove:
$AD = 2CD$.
Proof:
Since ABCD is a parallelogram, its opposite sides are parallel. Therefore, AD || BC.
Now, consider the parallel lines AD and BC and the transversal line AP that intersects them.
The alternate interior angles must be equal.
$\angle DAP = \angle APB$
[Alternate Interior Angles] ... (i)
We are given that AP is the bisector of $\angle A$.
$\angle DAP = \angle BAP$
[Given] ... (ii)
From equations (i) and (ii), we can conclude that:
$\angle APB = \angle BAP$
Now, in triangle $\triangle ABP$, we have two equal angles, $\angle APB$ and $\angle BAP$.
We know that in a triangle, the sides opposite to equal angles are also equal.
Therefore, the side opposite to $\angle APB$ (which is AB) must be equal to the side opposite to $\angle BAP$ (which is BP).
AB = BP
... (iii)
We are also given that P is the mid-point of the side BC.
$BC = 2 \times BP$
... (iv)
Substituting the value of BP from equation (iii) into equation (iv):
$BC = 2 \times AB$
... (v)
Since ABCD is a parallelogram, its opposite sides are equal.
$AD = BC$
$CD = AB$
Now, substituting these properties into equation (v):
$AD = 2CD$
Hence Proved.
Sample Question 1 to 4 (Before Exercise 8.4)
Sample Question 1: PQ and RS are two equal and parallel line-segments. Any point M not lying on PQ or RS is joined to Q and S and lines through P parallel to QM and through R parallel to SM meet at N. Prove that line segments MN and PQ are equal and parallel to each other.
Answer:
Given:
- PQ and RS are two line segments such that PQ = RS and PQ || RS.
- M is any point not lying on PQ or RS.
- A line is drawn through P parallel to QM, and a line is drawn through R parallel to SM.
- These two lines intersect at point N. So, PN || QM and RN || SM.
To Prove:
Line segments MN and PQ are equal and parallel to each other (MN = PQ and MN || PQ).
Proof:
It is given that PQ = RS and PQ || RS. A quadrilateral with one pair of opposite sides being equal and parallel is a parallelogram.
Therefore, PQRS is a parallelogram.
Since PQRS is a parallelogram, its other pair of opposite sides are also equal and parallel.
$PR = QS \text{ and } PR \ || \ QS$
... (i)
Now, since PR || QS and PQ is a transversal, the sum of the consecutive interior angles is $180^\circ$.
$\angle RPQ + \angle PQS = 180^\circ$
We can write $\angle PQS$ as the sum of $\angle PQM$ and $\angle MQS$.
$\angle RPQ + \angle PQM + \angle MQS = 180^\circ$
... (ii)
Also, it is given that PN || QM. With PQ as the transversal, the sum of consecutive interior angles is $180^\circ$.
$\angle NPQ + \angle PQM = 180^\circ$
We can write $\angle NPQ$ as the sum of $\angle NPR$ and $\angle RPQ$.
$\angle NPR + \angle RPQ + \angle PQM = 180^\circ$
... (iii)
Comparing equations (ii) and (iii), we get:
$\angle RPQ + \angle PQM + \angle MQS = \angle NPR + \angle RPQ + \angle PQM$
$\angle MQS = \angle NPR$
This can be written as:
$\angle NPR = \angle MQS$
... (iv)
Similarly, by considering PR || QS and the transversal RS, and also RN || SM and transversal RS, we can prove that:
$\angle NRP = \angle MSQ$
... (v)
Now, consider the triangles $\triangle PNR$ and $\triangle QMS$.
$\angle NPR = \angle MQS$
[From (iv)]
PR = QS
[From (i)]
$\angle NRP = \angle MSQ$
[From (v)]
By ASA (Angle-Side-Angle) congruence criterion:
$\triangle PNR \cong \triangle QMS$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
PN = QM
Now, consider the quadrilateral QMNP. We have:
PN = QM
(Proved above)
PN || QM
(Given)
Since one pair of opposite sides of quadrilateral QMNP is equal and parallel, it is a parallelogram.
The other pair of opposite sides of a parallelogram is also equal and parallel. Therefore:
MN = PQ and MN || PQ
Hence Proved.
Sample Question 2: Prove that a diagonal of a parallelogram divides it into two congruent triangles.
Answer:
Given:
A parallelogram ABCD and one of its diagonals, AC.
To Prove:
The diagonal AC divides the parallelogram into two congruent triangles, i.e., $\triangle ABC \cong \triangle CDA$.
Proof:
Since ABCD is a parallelogram, by definition, its opposite sides are parallel.
So, AB || DC and AD || BC.
Now, consider the diagonal AC as a transversal line that intersects the pair of parallel lines AB and DC.
$\angle BAC = \angle DCA$
[Alternate Interior Angles] ... (i)
Next, consider the diagonal AC as a transversal line that intersects the pair of parallel lines AD and BC.
$\angle DAC = \angle BCA$
[Alternate Interior Angles] ... (ii)
Now, let's compare the two triangles, $\triangle ABC$ and $\triangle CDA$.
$\angle BAC = \angle DCA$
[From (i)]
AC = CA
[Common side]
$\angle BCA = \angle DAC$
[From (ii)]
Therefore, by the ASA (Angle-Side-Angle) congruence criterion:
$\triangle ABC \cong \triangle CDA$
Thus, a diagonal of a parallelogram divides it into two congruent triangles.
Hence Proved.
Alternate Solution:
We know that the opposite sides of a parallelogram are equal in length.
So, in parallelogram ABCD, we have:
AB = CD and BC = DA.
Now, let's compare the two triangles, $\triangle ABC$ and $\triangle CDA$.
AB = CD
[Opposite sides of a parallelogram]
BC = DA
[Opposite sides of a parallelogram]
AC = CA
[Common side]
Therefore, by the SSS (Side-Side-Side) congruence criterion:
$\triangle ABC \cong \triangle CDA$
Hence Proved.
Sample Question 3: Show that the quadrilateral formed by joining the mid-points the sides of a rhombus, taken in order, form a rectangle.
Answer:
Given:
A rhombus ABCD. P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA respectively, joined in order to form a quadrilateral PQRS.
To Prove:
The quadrilateral PQRS is a rectangle.
Construction:
Join the diagonals of the rhombus, AC and BD.
Proof:
First, we will prove that PQRS is a parallelogram.
In $\triangle ABC$, P and Q are the mid-points of sides AB and BC, respectively.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
$PQ \ || \ AC \text{ and } PQ = \frac{1}{2}AC$
... (i)
Now, in $\triangle ADC$, R and S are the mid-points of sides CD and DA, respectively.
Again, by the Mid-point Theorem:
$SR \ || \ AC \text{ and } SR = \frac{1}{2}AC$
... (ii)
From equations (i) and (ii), we can conclude that:
$PQ \ || \ SR \text{ and } PQ = SR$
Since one pair of opposite sides of the quadrilateral PQRS is equal and parallel, PQRS is a parallelogram.
Now, we need to prove that one of the interior angles of this parallelogram is $90^\circ$.
In $\triangle ABD$, P and S are the mid-points of sides AB and DA, respectively.
By the Mid-point Theorem:
$PS \ || \ BD$
... (iii)
A key property of a rhombus is that its diagonals are perpendicular to each other.
$AC \perp BD$
From our results:
- $PQ \ || \ AC$ (from i)
- $PS \ || \ BD$ (from iii)
Since the sides of the angle $\angle SPQ$ (PQ and PS) are parallel to the perpendicular lines AC and BD, respectively, the angle $\angle SPQ$ must also be a right angle.
Therefore, $\angle SPQ = 90^\circ$.
Since PQRS is a parallelogram with one angle equal to $90^\circ$, it is a rectangle.
Hence Proved.
Sample Question 4: A diagonal of a parallelogram bisects one of its angle. Prove that it will bisect its opposite angle also.
Answer:
Given:
A parallelogram ABCD.
The diagonal AC bisects one of its angles, say $\angle A$.
To Prove:
The diagonal AC also bisects the opposite angle, $\angle C$.
Proof:
Since the diagonal AC bisects $\angle A$, we have:
$\angle DAC = \angle BAC$
(Given) ... (i)
ABCD is a parallelogram. By the properties of a parallelogram, its opposite sides are parallel.
1. Consider AB || DC and transversal AC:
The alternate interior angles are equal.
$\angle BAC = \angle DCA$
(Alternate Interior Angles) ... (ii)
2. Consider AD || BC and transversal AC:
The alternate interior angles are equal.
$\angle DAC = \angle BCA$
(Alternate Interior Angles) ... (iii)
From our given information in equation (i), we have $\angle DAC = \angle BAC$.
Now, we can substitute the values from equations (ii) and (iii) into equation (i).
Substituting $\angle DAC$ with $\angle BCA$ (from iii) and $\angle BAC$ with $\angle DCA$ (from ii), we get:
$\angle BCA = \angle DCA$
This shows that the diagonal AC divides $\angle C$ into two equal angles.
Therefore, the diagonal AC bisects its opposite angle $\angle C$.
Hence Proved.
Note on the shape:
From equations (i) and (ii), we can say $\angle DAC = \angle DCA$.
In $\triangle ADC$, since two angles are equal, the sides opposite to them must also be equal. So, $AD = DC$.
A parallelogram with adjacent sides equal is a rhombus. Therefore, the given parallelogram is a rhombus, and in a rhombus, the diagonals always bisect the angles.
Exercise 8.4
Question 1. A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.
Answer:
Given:
An isosceles right triangle, let's call it $\triangle ABC$, with the right angle at vertex A. So, $\angle A = 90^\circ$ and $AB = AC$.
A square is inscribed in $\triangle ABC$ such that they share the common angle A. Let the square be AFDE, where F lies on the side AB, E lies on the side AC, and the vertex D lies on the hypotenuse BC.
To Prove:
The vertex of the square opposite the common angle (which is D) bisects the hypotenuse BC.
That is, we need to prove that $BD = DC$.
Proof:
In the square AFDE, the diagonal is the line segment AD.
A property of a square is that its diagonal bisects the angles at the vertices.
The angle of the square at vertex A is $\angle FAE$, which is the same as $\angle BAC = 90^\circ$.
Therefore, the diagonal AD bisects $\angle FAE$.
$\angle FAD = \angle EAD = \frac{1}{2} \times 90^\circ = 45^\circ$
Since F lies on AB and E lies on AC, the angles $\angle FAD$ and $\angle EAD$ are the same as $\angle BAD$ and $\angle CAD$, respectively.
This means that the line segment AD is the angle bisector of $\angle BAC$ in $\triangle ABC$.
Now, we can apply the Angle Bisector Theorem to $\triangle ABC$.
The theorem states that if a line bisects an angle of a triangle, it divides the opposite side in the same ratio as the other two sides.
Applying this theorem for the angle bisector AD, we get:
$\frac{BD}{DC} = \frac{AB}{AC}$
... (i)
We are given that $\triangle ABC$ is an isosceles triangle with the right angle at A, which means the sides forming the right angle are equal.
AB = AC
(Given)
Substituting this equality into equation (i):
$\frac{BD}{DC} = \frac{AB}{AB} = 1$
$BD = DC$
This proves that D is the mid-point of the hypotenuse BC.
Hence Proved.
Question 2. In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
Answer:
Given:
A parallelogram ABCD in which:
- AB = 10 cm
- AD = 6 cm
The bisector of $\angle A$ intersects the side DC at E.
The lines AE and BC are produced to meet at a point F.
To Find:
The length of the line segment CF.
Solution:
Since ABCD is a parallelogram, its opposite sides are parallel and equal.
AD || BC
(Opposite sides of a parallelogram)
Since BC is produced to F, the entire line BF is parallel to AD.
AD || BF
Now, consider the parallel lines AD and BF and the transversal line AF that intersects them.
The alternate interior angles must be equal.
$\angle DAE = \angle BFA$ (or $\angle CFE$)
[Alternate Interior Angles] ... (i)
We are given that AE is the bisector of $\angle A$.
$\angle DAE = \angle BAE$
(Given) ... (ii)
From equations (i) and (ii), we can conclude that:
$\angle BFA = \angle BAE$
Now, in the triangle $\triangle ABF$, we have two equal angles, $\angle BFA$ and $\angle BAE$.
We know that in a triangle, the sides opposite to equal angles are also equal.
Therefore, the side opposite to $\angle BFA$ (which is AB) must be equal to the side opposite to $\angle BAE$ (which is BF).
BF = AB
We are given that AB = 10 cm, so BF = 10 cm.
The line segment BF is made up of two parts: BC and CF.
$BF = BC + CF$
In the parallelogram ABCD, the opposite sides are equal, so BC = AD = 6 cm.
Substituting the known values:
$10 \text{ cm} = 6 \text{ cm} + CF$
$CF = 10 \text{ cm} - 6 \text{ cm}$
$CF = 4 \text{ cm}$
Therefore, the length of CF is 4 cm.
Alternate Solution:
Since ABCD is a parallelogram, AB || DC. Since E lies on DC, we have AB || DE.
Consider the parallel lines AB and DE and the transversal line AE.
$\angle BAE = \angle AED$
(Alternate Interior Angles) ... (iii)
We are given that AE bisects $\angle A$, so:
$\angle DAE = \angle BAE$
(Given) ... (iv)
From (iii) and (iv), we get $\angle DAE = \angle AED$.
In $\triangle ADE$, since two angles are equal, the sides opposite them are equal. So, $DE = AD$.
We are given AD = 6 cm, so $DE = 6 \text{ cm}$.
The full length of the side DC is equal to the opposite side AB, so $DC = 10 \text{ cm}$.
We can find the length of CE: $CE = DC - DE = 10 \text{ cm} - 6 \text{ cm} = 4 \text{ cm}$.
Now, consider $\triangle ADE$ and $\triangle FCE$.
$\angle AED = \angle FEC$
(Vertically opposite angles)
$\angle DAE = \angle CFE$
(Alternate interior angles, since AD || BF)
By AA similarity criterion, $\triangle ADE \sim \triangle FCE$.
The ratio of corresponding sides must be equal:
$\frac{AD}{CF} = \frac{DE}{CE} = \frac{AE}{FE}$
Using the first two parts of the ratio:
$\frac{AD}{CF} = \frac{DE}{CE}$
Substituting the known values ($AD = 6, DE = 6, CE = 4$):
$\frac{6}{CF} = \frac{6}{4}$
This implies that $CF = 4 \text{ cm}$.
Question 3. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
Answer:
Given:
A quadrilateral ABCD.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA, respectively.
The diagonals of the quadrilateral ABCD are equal, i.e., AC = BD.
To Prove:
The quadrilateral PQRS is a rhombus.
Construction:
Join the diagonals AC and BD of the quadrilateral ABCD.
Proof:
First, we will prove that PQRS is a parallelogram using the Mid-point Theorem.
The Mid-point Theorem states that the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
In $\triangle ABC$, P and Q are the mid-points of sides AB and BC, respectively.
By the Mid-point Theorem:
$PQ \ || \ AC \text{ and } PQ = \frac{1}{2}AC$
... (i)
In $\triangle ADC$, S and R are the mid-points of sides DA and CD, respectively.
By the Mid-point Theorem:
$SR \ || \ AC \text{ and } SR = \frac{1}{2}AC$
... (ii)
From equations (i) and (ii), we can conclude that:
$PQ \ || \ SR \text{ and } PQ = SR$
Since one pair of opposite sides of the quadrilateral PQRS is equal and parallel, PQRS is a parallelogram.
Now, we need to prove that the adjacent sides of this parallelogram are equal.
In $\triangle ABD$, P and S are the mid-points of sides AB and DA, respectively.
By the Mid-point Theorem:
$PS \ || \ BD \text{ and } PS = \frac{1}{2}BD$
... (iii)
We are given that the diagonals of the quadrilateral ABCD are equal.
$AC = BD$
(Given)
Multiplying both sides by $\frac{1}{2}$:
$\frac{1}{2}AC = \frac{1}{2}BD$
From equations (i) and (iii), we know that $PQ = \frac{1}{2}AC$ and $PS = \frac{1}{2}BD$.
Substituting these into the above equality, we get:
$PQ = PS$
Since PQRS is a parallelogram in which a pair of adjacent sides (PQ and PS) are equal, it must be a rhombus.
Therefore, PQRS is a rhombus.
Hence Proved.
Question 4. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
Answer:
Given:
A quadrilateral ABCD.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA, respectively.
The diagonals of the quadrilateral ABCD are perpendicular to each other, i.e., AC $\perp$ BD.
To Prove:
The quadrilateral PQRS is a rectangle.
Construction:
Join the diagonals AC and BD of the quadrilateral ABCD.
Proof:
First, we will prove that PQRS is a parallelogram using the Mid-point Theorem.
The Mid-point Theorem states that the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
In $\triangle ABC$, P and Q are the mid-points of sides AB and BC, respectively.
By the Mid-point Theorem:
$PQ \ || \ AC$
... (i)
In $\triangle ADC$, S and R are the mid-points of sides DA and CD, respectively.
By the Mid-point Theorem:
$SR \ || \ AC$
... (ii)
From equations (i) and (ii), we can conclude that $PQ \ || \ SR$.
Similarly, in $\triangle ABD$, P and S are the mid-points of sides AB and DA, respectively.
By the Mid-point Theorem:
$PS \ || \ BD$
... (iii)
Since both pairs of opposite sides of the quadrilateral PQRS are parallel, PQRS is a parallelogram.
Now, we need to prove that one of the interior angles of this parallelogram is $90^\circ$.
Let the diagonals AC and BD intersect at a point O.
Let the line PS intersect AC at M and PQ intersect BD at N.
From our results:
- $PQ \ || \ AC$ (from i)
- $PS \ || \ BD$ (from iii)
Since PS || BD (which is the same as ON), and PQ || AC (which is the same as OM), the quadrilateral PMON is a parallelogram.
The angle at the vertex P of the parallelogram PQRS is $\angle SPQ$. This is the same as the angle $\angle MPN$ of the smaller parallelogram PMON.
The angle opposite to $\angle MPN$ in the parallelogram PMON is $\angle MON$. Opposite angles of a parallelogram are equal.
$\angle SPQ = \angle MON$
The angle $\angle MON$ is the angle between the diagonals AC and BD of the original quadrilateral. We are given that these diagonals are perpendicular.
$AC \perp BD \implies \angle MON = 90^\circ$
Therefore, $\angle SPQ = 90^\circ$.
Since PQRS is a parallelogram with one angle equal to $90^\circ$, it is a rectangle.
Hence Proved.
Question 5. P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove that PQRS is a square.
Answer:
Given:
A quadrilateral ABCD.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA, respectively.
The diagonals of the quadrilateral ABCD are equal and perpendicular, i.e., $AC = BD$ and $AC \perp BD$.
To Prove:
The quadrilateral PQRS is a square.
Construction:
Join the diagonals AC and BD of the quadrilateral ABCD.
Proof:
The proof involves two main steps: first, proving that PQRS is a rhombus, and second, proving that it is a rectangle. A quadrilateral that is both a rhombus and a rectangle is a square.
Step 1: Proving PQRS is a Rhombus
In $\triangle ABC$, P and Q are the mid-points of sides AB and BC, respectively.
By the Mid-point Theorem:
$PQ = \frac{1}{2}AC$
... (i)
In $\triangle ABD$, P and S are the mid-points of sides AB and DA, respectively.
By the Mid-point Theorem:
$PS = \frac{1}{2}BD$
... (ii)
Similarly, in $\triangle BCD$ and $\triangle ADC$, we get:
$QR = \frac{1}{2}BD$ and $SR = \frac{1}{2}AC$.
We are given that the diagonals of ABCD are equal:
$AC = BD$
Multiplying by $\frac{1}{2}$, we get $\frac{1}{2}AC = \frac{1}{2}BD$.
From our findings above, we can substitute the side lengths of PQRS:
$PQ = PS = QR = SR$
Since all four sides of the quadrilateral PQRS are equal, it is a rhombus.
Step 2: Proving PQRS is a Rectangle
From the Mid-point Theorem, we also know the parallel relationships:
In $\triangle ABC$, $PQ \ || \ AC$.
In $\triangle ABD$, $PS \ || \ BD$.
We are given that the diagonals of ABCD are perpendicular:
$AC \perp BD$
Since the sides of the angle $\angle SPQ$ (PQ and PS) are parallel to the two perpendicular lines AC and BD, respectively, the angle $\angle SPQ$ must also be a right angle.
$\angle SPQ = 90^\circ$
Since PQRS is a quadrilateral with all sides equal (a rhombus) and one interior angle equal to $90^\circ$, it must be a rectangle as well.
Step 3: Conclusion
A quadrilateral that is both a rhombus (all sides equal) and a rectangle (all angles are $90^\circ$) is a square.
Therefore, PQRS is a square.
Hence Proved.
Question 6. A diagonal of a parallelogram bisects one of its angles. Show that it is a rhombus.
Answer:
Given:
A parallelogram ABCD.
The diagonal AC bisects one of its angles, $\angle A$.
To Prove:
The parallelogram ABCD is a rhombus.
Proof:
To prove that the parallelogram ABCD is a rhombus, we need to show that its adjacent sides are equal (e.g., AB = AD).
Since the diagonal AC bisects $\angle A$, we have:
$\angle DAC = \angle BAC$
(Given) ... (i)
Because ABCD is a parallelogram, its opposite sides are parallel. So, AB || DC.
Now, consider the parallel lines AB and DC and the transversal line AC that intersects them.
The alternate interior angles are equal.
$\angle BAC = \angle DCA$
(Alternate Interior Angles) ... (ii)
From equations (i) and (ii), by comparing the angles, we can conclude that:
$\angle DAC = \angle DCA$
Now, let's consider the triangle $\triangle ADC$.
We have just shown that two of its angles, $\angle DAC$ and $\angle DCA$, are equal. In a triangle, the sides opposite to equal angles are also equal.
The side opposite to $\angle DCA$ is AD.
The side opposite to $\angle DAC$ is DC.
Therefore:
AD = DC
(Sides opposite to equal angles are equal)
In a parallelogram, we know that the opposite sides are equal.
So, AB = DC and AD = BC.
Since we have proved that the adjacent sides AD and DC are equal, it follows that all four sides are equal:
$AB = BC = CD = DA$
A parallelogram with all four sides equal is, by definition, a rhombus.
Therefore, the parallelogram ABCD is a rhombus.
Hence Proved.
Question 7. P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
Answer:
Given:
A parallelogram ABCD.
- P is the mid-point of the side AB.
- Q is the mid-point of the side CD.
- AQ intersects DP at S.
- BQ intersects CP at R.
To Prove:
The quadrilateral PRQS is a parallelogram.
Proof:
The proof strategy is to first demonstrate that two larger quadrilaterals, APCQ and BQDP, are parallelograms. This will establish that their opposite sides are parallel, which will in turn help us prove that PRQS is a parallelogram.
Step 1: Prove that APCQ is a parallelogram.
Since ABCD is a parallelogram, we know that its opposite sides are equal and parallel.
$AB = CD \text{ and } AB \ || \ CD$
Since P is the mid-point of AB and Q is the mid-point of CD:
$AP = \frac{1}{2}AB$
$QC = \frac{1}{2}CD$
Because AB = CD, it follows that their halves are also equal:
$AP = QC$
... (i)
Also, since AB || CD, their parts are also parallel:
$AP \ || \ QC$
... (ii)
In the quadrilateral APCQ, from (i) and (ii), we have one pair of opposite sides (AP and QC) that are both equal and parallel. A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, APCQ is a parallelogram.
A property of a parallelogram is that its opposite sides are parallel. So, we have:
$AQ \ || \ PC$
... (iii)
Step 2: Prove that BQDP is a parallelogram.
From the properties of parallelogram ABCD and the mid-points P and Q, we also have:
$PB = \frac{1}{2}AB$
$QD = \frac{1}{2}CD$
Since AB = CD, it follows that:
$PB = QD$
... (iv)
And since AB || CD, their parts are also parallel:
$PB \ || \ QD$
... (v)
In the quadrilateral BQDP, from (iv) and (v), we have one pair of opposite sides (PB and QD) that are both equal and parallel.
Therefore, BQDP is a parallelogram.
A property of a parallelogram is that its opposite sides are parallel. So, we have:
$DP \ || \ QB$
... (vi)
Step 3: Prove that PRQS is a parallelogram.
Now, let's consider the quadrilateral PRQS.
- S is a point on the line segment AQ.
- R is a point on the line segment PC.
- From (iii), we know that AQ || PC. Therefore, their parts must also be parallel: SQ || PR.
- S is a point on the line segment DP.
- R is a point on the line segment QB.
- From (vi), we know that DP || QB. Therefore, their parts must also be parallel: SP || RQ.
Since both pairs of opposite sides of the quadrilateral PRQS are parallel (SQ || PR and SP || RQ), by definition, PRQS is a parallelogram.
Hence Proved.
Question 8. ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that ∠A = ∠B and ∠C = ∠D.
Answer:
Given:
A quadrilateral ABCD in which:
- AB || DC (which means it's a trapezium).
- AD = BC (the non-parallel sides are equal, so it's an isosceles trapezium).
To Prove:
The base angles are equal, i.e., $\angle A = \angle B$ and $\angle C = \angle D$.
Construction:
Draw a line segment from C parallel to AD, which intersects the line AB at point E.
Proof:
Step 1: Analyze quadrilateral AECD and $\triangle CEB$.
In the quadrilateral AECD:
AE || DC
(Part of AB which is parallel to DC)
AD || EC
(By construction)
Since both pairs of opposite sides are parallel, AECD is a parallelogram.
By the properties of a parallelogram, opposite sides are equal.
AD = EC
... (i)
We are given that AD = BC.
From (i) and the given information, we can conclude that:
BC = EC
Since two sides of $\triangle CEB$ are equal, it is an isosceles triangle. In an isosceles triangle, the angles opposite to the equal sides are also equal.
$\angle CEB = \angle CBE$ (which is $\angle B$)
... (ii)
Step 2: Prove $\angle A = \angle B$.
Since AD || EC (by construction) and AEB is a transversal line:
$\angle A = \angle CEB$
(Corresponding angles are equal)
From equation (ii), we know that $\angle CEB = \angle B$.
Therefore, we can conclude that $\angle A = \angle B$. (First part proved)
Step 3: Prove $\angle C = \angle D$.
Since AB || DC, the sum of consecutive interior angles on the same side of the transversals AD and BC is $180^\circ$.
$\angle A + \angle D = 180^\circ$
... (iii)
$\angle B + \angle C = 180^\circ$
... (iv)
From (iii) and (iv), we have:
$\angle A + \angle D = \angle B + \angle C$
Since we have already proved that $\angle A = \angle B$, we can cancel these terms from both sides of the equation.
$\angle D = \angle C$. (Second part proved)
Hence Proved.
Question 9. In Fig. 8.11, AB || DE, AB = DE, AC || DF and AC = DF. Prove that BC || EF and BC = EF.

Answer:
Given:
- AB || DE and AB = DE
- AC || DF and AC = DF
To Prove:
BC || EF and BC = EF.
Proof:
The proof involves showing that several quadrilaterals in the figure are parallelograms.
Step 1: Prove that quadrilateral ABED is a parallelogram.
In the quadrilateral ABED, we are given that one pair of opposite sides, AB and DE, are equal and parallel.
AB = DE
(Given)
AB || DE
(Given)
A quadrilateral is a parallelogram if one pair of its opposite sides is equal and parallel.
Therefore, ABED is a parallelogram.
Since ABED is a parallelogram, its other pair of opposite sides (AD and BE) must also be equal and parallel.
AD = BE and AD || BE
... (i)
Step 2: Prove that quadrilateral ACFD is a parallelogram.
In the quadrilateral ACFD, we are given that one pair of opposite sides, AC and DF, are equal and parallel.
AC = DF
(Given)
AC || DF
(Given)
Therefore, ACFD is a parallelogram.
Since ACFD is a parallelogram, its other pair of opposite sides (AD and CF) must also be equal and parallel.
AD = CF and AD || CF
... (ii)
Step 3: Compare results from Step 1 and Step 2.
From equation (i), we have: $AD = BE$ and $AD \ || \ BE$.
From equation (ii), we have: $AD = CF$ and $AD \ || \ CF$.
By comparing these two results, we can conclude:
$BE = CF$ (since both are equal to AD)
$BE \ || \ CF$ (since both are parallel to AD)
Step 4: Prove that quadrilateral BCFE is a parallelogram.
In the quadrilateral BCFE, we have just proved in Step 3 that one pair of opposite sides, BE and CF, are equal and parallel.
Therefore, BCFE is a parallelogram.
Since BCFE is a parallelogram, its other pair of opposite sides, BC and EF, must also be equal and parallel.
BC = EF and BC || EF
Hence Proved.
Question 10. E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = $\frac{1}{3}$ AC.
Answer:
Given:
In $\triangle ABC$:
- AD is a median, which means D is the mid-point of BC.
- E is the mid-point of the median AD.
- The line segment BE is produced (extended) to meet the side AC at a point F.
To Prove:
$AF = \frac{1}{3} AC$.
Construction:
Draw a line segment through the point D, parallel to BF (or BEF), that intersects the side AC at a point G. So, DG || BF.
Proof:
The proof relies on applying the Converse of the Mid-point Theorem twice.
The Converse of the Mid-point Theorem states that a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Step 1: Apply the theorem to $\triangle ADG$.
In the triangle $\triangle ADG$:
- E is the mid-point of the side AD. (Given)
- The line segment EF is part of BF, and by our construction, DG || BF. Therefore, EF || DG.
By applying the Converse of the Mid-point Theorem to $\triangle ADG$, the line EF must bisect the third side, AG.
Therefore, F is the mid-point of AG.
AF = FG
... (i)
Step 2: Apply the theorem to $\triangle CBF$.
In the triangle $\triangle CBF$:
- D is the mid-point of the side CB. (Given, since AD is a median)
- The line segment DG is parallel to the side BF. (By construction)
By applying the Converse of the Mid-point Theorem to $\triangle CBF$, the line DG must bisect the third side, CF.
Therefore, G is the mid-point of CF.
FG = GC
... (ii)
Step 3: Combine the results.
From equation (i), we have AF = FG.
From equation (ii), we have FG = GC.
Combining these two results, we get:
AF = FG = GC
This means that the points F and G divide the line segment AC into three equal parts.
The total length of the side AC can be written as the sum of these three parts:
$AC = AF + FG + GC$
Since all three parts are equal to AF, we can substitute them:
$AC = AF + AF + AF$
$AC = 3 \times AF$
Rearranging this equation to make AF the subject, we get:
$AF = \frac{1}{3} AC$
Hence Proved.
Question 11. Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
Answer:
Given:
A square ABCD.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA, respectively, joined in order to form a quadrilateral PQRS.
To Prove:
The quadrilateral PQRS is a square.
Construction:
Join the diagonals AC and BD of the square ABCD.
Proof:
The proof involves two main steps: first, proving that PQRS is a rhombus by showing its sides are equal, and second, proving that it is a rectangle by showing its angles are 90°. A quadrilateral that is both a rhombus and a rectangle is a square.
Step 1: Proving PQRS is a Rhombus
Let the side length of the square ABCD be 'a'. So, AB = BC = CD = DA = a.
Since P, Q, R, and S are mid-points:
$AP = PB = BQ = QC = CR = RD = DS = SA = \frac{a}{2}$
Now consider the four right-angled triangles at the corners of the square: $\triangle APS, \triangle BPQ, \triangle CRQ,$ and $\triangle DRS$.
In $\triangle APS$:
$PS^2 = AP^2 + AS^2 = (\frac{a}{2})^2 + (\frac{a}{2})^2 = \frac{a^2}{4} + \frac{a^2}{4} = \frac{2a^2}{4} = \frac{a^2}{2}$
In $\triangle BPQ$:
$PQ^2 = PB^2 + BQ^2 = (\frac{a}{2})^2 + (\frac{a}{2})^2 = \frac{a^2}{2}$
In $\triangle CRQ$:
$QR^2 = QC^2 + CR^2 = (\frac{a}{2})^2 + (\frac{a}{2})^2 = \frac{a^2}{2}$
In $\triangle DRS$:
$RS^2 = RD^2 + DS^2 = (\frac{a}{2})^2 + (\frac{a}{2})^2 = \frac{a^2}{2}$
Since $PS^2 = PQ^2 = QR^2 = RS^2$, their lengths must be equal:
$PS = PQ = QR = RS$
As all four sides of the quadrilateral PQRS are equal, it is a rhombus.
Step 2: Proving PQRS is a Rectangle
We will use the Mid-point Theorem. In $\triangle ABC$, P and Q are mid-points.
$PQ \ || \ AC$
In $\triangle ABD$, P and S are mid-points.
$PS \ || \ BD$
A property of a square is that its diagonals are perpendicular to each other.
$AC \perp BD$
Since the adjacent sides of PQRS (PQ and PS) are parallel to the perpendicular diagonals of the square (AC and BD), the sides PQ and PS must also be perpendicular to each other.
$\angle SPQ = 90^\circ$
A rhombus with one angle equal to $90^\circ$ is a square. So PQRS is a rectangle as well.
Step 3: Conclusion
Since PQRS is both a rhombus (all sides equal) and a rectangle (all angles 90°), PQRS is a square.
Hence Proved.
Question 12. E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = $\frac{1}{2}$ (AB + CD).
[Hint: Join BE and produce it to meet CD produced at G.]
Answer:
Given:
A trapezium ABCD with AB || DC.
E is the mid-point of the non-parallel side AD.
F is the mid-point of the non-parallel side BC.
To Prove:
1. EF || AB
2. $EF = \frac{1}{2} (AB + CD)$
Construction:
Join the line segment BE and produce (extend) it to meet the line CD produced at a point G.
Proof:
The proof involves proving the congruence of two triangles and then applying the Mid-point Theorem.
Step 1: Prove $\triangle ABE \cong \triangle DGE$.
In $\triangle ABE$ and $\triangle DGE$:
AE = DE
(Given that E is the mid-point of AD)
$\angle AEB = \angle DEG$
(Vertically opposite angles)
Since AB || DC, and CG is the extension of DC, we have AB || CG. With the transversal line AG, the alternate interior angles are equal.
$\angle BAE = \angle GDE$
(Alternate interior angles)
Therefore, by ASA (Angle-Side-Angle) congruence criterion:
$\triangle ABE \cong \triangle DGE$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
AB = DG
... (i)
BE = EG
... (ii)
Equation (ii) shows that E is the mid-point of the line segment BG.
Step 2: Apply the Mid-point Theorem to $\triangle BCG$.
In the triangle $\triangle BCG$:
- F is the mid-point of the side BC. (Given)
- E is the mid-point of the side BG. (Proved in Step 1)
According to the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
Therefore:
$EF \ || \ CG \text{ and } EF = \frac{1}{2} CG$
Step 3: Conclude the proof.
Since $EF \ || \ CG$, and CG is the same line as DC, we have $EF \ || \ DC$.
We are given that $DC \ || \ AB$.
Since EF is parallel to DC and DC is parallel to AB, we can conclude that EF || AB. (First part proved)
Now, for the length of EF:
$EF = \frac{1}{2} CG$
The length of the line segment CG can be written as the sum of CD and DG.
$CG = CD + DG$
From our congruence result in equation (i), we know that $DG = AB$.
Substituting this into the expression for CG:
$CG = CD + AB$
Now, substitute this back into the equation for EF:
$EF = \frac{1}{2} (CD + AB)$ (Second part proved)
Hence Proved.
Question 13. Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
Answer:
Given:
A parallelogram ABCD.
The bisectors of the interior angles $\angle A, \angle B, \angle C,$ and $\angle D$ intersect to form a quadrilateral PQRS.
To Prove:
The quadrilateral PQRS is a rectangle.
Proof:
To prove that PQRS is a rectangle, we need to show that all its interior angles are equal to $90^\circ$.
We know that in a parallelogram, the adjacent angles are supplementary (their sum is $180^\circ$).
Step 1: Find the measure of $\angle PSR$.
Consider the adjacent angles $\angle A$ and $\angle D$ of the parallelogram ABCD.
$\angle A + \angle D = 180^\circ$
(Adjacent angles of a parallelogram)
The bisectors of $\angle A$ and $\angle D$ meet at point S. So, AS is the bisector of $\angle A$ and DS is the bisector of $\angle D$.
$\angle DAS = \frac{1}{2}\angle A$
$\angle ADS = \frac{1}{2}\angle D$
Now, consider the triangle $\triangle ADS$. By the angle sum property of a triangle:
$\angle ASD + \angle DAS + \angle ADS = 180^\circ$
$\angle ASD + \frac{1}{2}\angle A + \frac{1}{2}\angle D = 180^\circ$
$\angle ASD + \frac{1}{2}(\angle A + \angle D) = 180^\circ$
Substituting the value of $(\angle A + \angle D)$:
$\angle ASD + \frac{1}{2}(180^\circ) = 180^\circ$
$\angle ASD + 90^\circ = 180^\circ$
$\angle ASD = 90^\circ$
The angle $\angle PSR$ is vertically opposite to the angle $\angle ASD$.
Therefore, $\angle PSR = \angle ASD = 90^\circ$.
Step 2: Find the measure of $\angle SPQ$.
Consider the adjacent angles $\angle A$ and $\angle B$ of the parallelogram ABCD.
$\angle A + \angle B = 180^\circ$
(Adjacent angles of a parallelogram)
The bisectors of $\angle A$ and $\angle B$ meet at point P. So, AP is the bisector of $\angle A$ and BP is the bisector of $\angle B$.
In $\triangle APB$:
$\angle APB + \angle PAB + \angle PBA = 180^\circ$
$\angle APB + \frac{1}{2}\angle A + \frac{1}{2}\angle B = 180^\circ$
$\angle APB + \frac{1}{2}(\angle A + \angle B) = 180^\circ$
$\angle APB + \frac{1}{2}(180^\circ) = 180^\circ$
$\angle APB = 90^\circ$
The angle $\angle SPQ$ is vertically opposite to the angle $\angle APB$.
Therefore, $\angle SPQ = \angle APB = 90^\circ$.
Step 3: Conclusion.
Similarly, we can prove that $\angle PQR = 90^\circ$ (by considering $\triangle BQC$) and $\angle QRS = 90^\circ$ (by considering $\triangle CRD$).
Since all four interior angles of the quadrilateral PQRS are $90^\circ$, it is a rectangle.
Hence Proved.
Question 14. P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
Answer:
Given:
A parallelogram ABCD.
The diagonals AC and BD intersect at the point O.
P is a point on the side AD and Q is a point on the opposite side BC.
The line segment PQ passes through the point O.
To Prove:
The line segment PQ is bisected at O (i.e., PO = QO).
Proof:
To prove that PO = QO, we will prove the congruence of the triangles formed by these segments.
Let's consider the triangles $\triangle POA$ and $\triangle QOC$.
Since ABCD is a parallelogram, we know its properties:
1. The diagonals bisect each other. Therefore, O is the midpoint of AC.
OA = OC
... (i)
2. The opposite sides are parallel. So, AD || BC.
Now, considering AD || BC and the transversal line AC that intersects them:
$\angle PAO = \angle QCO$
[Alternate Interior Angles] ... (ii)
The angles $\angle POA$ and $\angle QOC$ are formed by the intersection of lines AC and PQ.
$\angle POA = \angle QOC$
[Vertically Opposite Angles] ... (iii)
Now, in $\triangle POA$ and $\triangle QOC$:
$\angle PAO = \angle QCO$
[From (ii)]
OA = OC
[From (i)]
$\angle POA = \angle QOC$
[From (iii)]
Therefore, by ASA (Angle-Side-Angle) congruence criterion:
$\triangle POA \cong \triangle QOC$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), the corresponding sides must be equal.
PO = QO
Since PO = QO, the point O is the midpoint of the line segment PQ.
Thus, PQ is bisected at O.
Hence Proved.
Question 15. ABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
Answer:
Given:
A rectangle ABCD.
The diagonal BD bisects $\angle B$.
To Prove:
The rectangle ABCD is a square.
Proof:
To prove that the rectangle ABCD is a square, we need to show that its adjacent sides are equal in length (e.g., AB = BC).
Since the diagonal BD bisects $\angle B$, we have:
$\angle ABD = \angle CBD$
(Given) ... (i)
Because ABCD is a rectangle, it is also a parallelogram. Therefore, its opposite sides are parallel. So, AB || DC.
Now, consider the parallel lines AB and DC and the transversal line BD that intersects them.
The alternate interior angles are equal.
$\angle ABD = \angle BDC$
(Alternate Interior Angles) ... (ii)
From equations (i) and (ii), by comparing the angles, we can conclude that:
$\angle CBD = \angle BDC$
Now, let's consider the triangle $\triangle BCD$.
We have just shown that two of its angles, $\angle CBD$ and $\angle BDC$, are equal. In a triangle, the sides opposite to equal angles are also equal.
The side opposite to $\angle BDC$ is BC.
The side opposite to $\angle CBD$ is CD.
Therefore:
BC = CD
(Sides opposite to equal angles are equal)
In a rectangle, we know that the opposite sides are equal.
So, AB = CD and BC = AD.
Since we have proved that the adjacent sides BC and CD are equal, it follows that all four sides are equal:
$AB = BC = CD = DA$
A rectangle in which all four sides are equal is, by definition, a square.
Therefore, the rectangle ABCD is a square.
Hence Proved.
Question 16. D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
Answer:
Given:
In a triangle ABC, D, E and F are the mid-points of the sides AB, BC and CA respectively.
To Prove:
By joining the mid-points D, E, and F, the triangle ABC is divided into four congruent triangles. That is, $ΔADF ≅ ΔBDE ≅ ΔCEF ≅ ΔDEF$.
Proof:
We will use the Mid-point Theorem, which states that the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
Since D and F are the mid-points of sides AB and AC respectively in $ΔABC$:
DF $||$ BC and DF $= \frac{1}{2}$ BC
(By Mid-point Theorem)
As E is the mid-point of BC, this implies DF $||$ BE and DF = BE.
Similarly, since D and E are the mid-points of sides AB and BC respectively:
DE $||$ AC and DE $= \frac{1}{2}$ AC
(By Mid-point Theorem)
As F is the mid-point of AC, this implies DE $||$ FC and DE = FC.
And, since E and F are the mid-points of sides BC and AC respectively:
EF $||$ AB and EF $= \frac{1}{2}$ AB
(By Mid-point Theorem)
As D is the mid-point of AB, this implies EF $||$ AD and EF = AD.
Now, consider the quadrilateral BDFE.
DF $||$ BE and DF = BE
(Proved above)
EF $||$ BD and EF = BD
(Proved above)
Since both pairs of opposite sides are parallel and equal, BDFE is a parallelogram.
A diagonal of a parallelogram divides it into two congruent triangles. Here, DE is a diagonal of parallelogram BDFE.
$ΔBDE ≅ ΔFED$
... (i)
Similarly, we can prove that DFCE is a parallelogram. FE is its diagonal.
$ΔCEF ≅ ΔDFE$
... (ii)
And, we can also prove that AFDE is a parallelogram. DF is its diagonal.
$ΔADF ≅ ΔEFD$
... (iii)
From equations (i), (ii), and (iii), we see that all three triangles ($ΔBDE$, $ΔCEF$, $ΔADF$) are congruent to $ΔDEF$.
Therefore, all four triangles are congruent to each other.
Hence, $ΔADF ≅ ΔBDE ≅ ΔCEF ≅ ΔDEF$.
Thus, joining the mid-points D, E, and F divides the triangle ABC into four congruent triangles.
Alternate Solution (Using SSS Congruence Rule)
From the Mid-point Theorem, we know:
1. $DF = \frac{1}{2} BC = BE = EC$
2. $DE = \frac{1}{2} AC = AF = FC$
3. $EF = \frac{1}{2} AB = AD = DB$
Now, we can prove the congruence of all four triangles using the SSS (Side-Side-Side) congruence criterion.
Comparing $ΔADF$ and $ΔDEF$:
AD = EF (from point 3)
AF = DE (from point 2)
DF = FD (Common side)
So, by SSS congruence, $ΔADF ≅ ΔEFD$.
Comparing $ΔBDE$ and $ΔDEF$:
BD = EF (from point 3)
BE = DF (from point 1)
DE = ED (Common side)
So, by SSS congruence, $ΔBDE ≅ ΔFED$.
Comparing $ΔCEF$ and $ΔDEF$:
CE = DF (from point 1)
CF = DE (from point 2)
EF = FE (Common side)
So, by SSS congruence, $ΔCEF ≅ ΔDFE$.
Since $ΔADF$, $ΔBDE$, and $ΔCEF$ are all congruent to $ΔDEF$, they are all congruent to each other.
Hence, $ΔADF ≅ ΔBDE ≅ ΔCEF ≅ ΔDEF$.
Question 17. Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
Answer:
Given:
A trapezium ABCD in which AB $||$ DC. P and Q are the mid-points of the diagonals AC and BD respectively.
To Prove:
The line segment PQ is parallel to the parallel sides AB and DC. That is, PQ $||$ AB and PQ $||$ DC.
Construction Required:
Join DP and extend it to intersect the side AB at a point R.
Proof:
We consider the triangles $Δ$APR and $Δ$DPC.
AP = PC
(P is the mid-point of AC)
$\angle$RAP = $\angle$DCP
(Alternate interior angles, as AB $||$ DC and AC is the transversal)
$\angle$APR = $\angle$DPC
(Vertically opposite angles)
Therefore, by the ASA (Angle-Side-Angle) congruence criterion:
$Δ$APR $≅$ $Δ$DPC
By CPCTC (Corresponding Parts of Congruent Triangles are Corresponding):
DP = PR
... (i)
This means that P is the mid-point of the line segment DR.
Now, consider the triangle $Δ$DRB.
P is the mid-point of DR
(From (i))
Q is the mid-point of DB
(Given)
According to the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
So, in $Δ$DRB, the line segment PQ is parallel to the third side RB.
PQ $||$ RB
Since RB is a part of the line AB, we have:
PQ $||$ AB
We are given that AB $||$ DC.
Since PQ is parallel to AB and AB is parallel to DC, it follows that PQ is also parallel to DC.
PQ $||$ DC
Hence, the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
Hence Proved.
Alternate Solution:
Given: A trapezium ABCD with AB $||$ DC. P and Q are the mid-points of diagonals AC and BD respectively.
To Prove: PQ $||$ AB and PQ $||$ DC.
Construction: Join C and Q, and extend it to meet AB at point R.
Proof:
Consider the triangles $Δ$DQC and $Δ$BQR.
DQ = QB
(Q is the mid-point of BD)
$\angle$CDQ = $\angle$RBQ
(Alternate interior angles, as DC $||$ AR and BD is the transversal)
$\angle$DQC = $\angle$BQR
(Vertically opposite angles)
Therefore, by the ASA (Angle-Side-Angle) congruence criterion:
$Δ$DQC $≅$ $Δ$BQR
By CPCTC, we have:
CQ = QR
This shows that Q is the mid-point of the line segment CR.
Now, consider the triangle $Δ$CAR.
P is the mid-point of AC
(Given)
Q is the mid-point of CR
(Proved above)
By the Mid-point Theorem in $Δ$CAR, the line segment PQ joining the mid-points of sides AC and CR must be parallel to the third side AR.
PQ $||$ AR
Since AR is a part of the line AB, we have:
PQ $||$ AB
Also, since we are given AB $||$ DC, we can conclude that:
PQ $||$ DC
Hence Proved.
Question 18. P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
Answer:
Given:
ABCD is a parallelogram.
P is the mid-point of the side CD, so DP = PC.
A line through C is parallel to PA, which intersects AB at Q and DA produced at R. So, PA $||$ RC.
To Prove:
1. DA = AR
2. CQ = QR
Proof:
1. To prove DA = AR
Consider the triangle $Δ$DCR.
P is the mid-point of side DC.
(Given)
PA $||$ CR
(Given)
According to the Converse of the Mid-point Theorem, the line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
In $Δ$DCR, the line PA starts from P (the mid-point of DC) and is parallel to the side CR. It intersects the third side DR at point A.
Therefore, A must be the mid-point of DR.
This implies that DA = AR.
Hence, the first part is proved.
2. To prove CQ = QR
Since ABCD is a parallelogram, the opposite sides are parallel and equal.
AD $||$ BC and AD = BC
(Properties of a parallelogram)
Since AD is produced to R, the line segment DR is parallel to BC. Consequently, AR is also parallel to BC (AR $||$ BC).
From the first part, we proved that DA = AR.
Since DA = BC, it follows that AR = BC.
Now, let's consider the triangles $Δ$AQR and $Δ$BQC.
$\angle$AQR = $\angle$BQC
(Vertically opposite angles)
AR = BC
(Proved above)
Since AR $||$ BC and RC is the transversal line that intersects them:
$\angle$ARQ = $\angle$BCQ
(Alternate interior angles)
So, by the AAS (Angle-Angle-Side) congruence criterion:
$Δ$AQR $≅$ $Δ$BQC
By CPCTC (Corresponding Parts of Congruent Triangles are Corresponding), the corresponding sides must be equal.
Therefore, CQ = QR.
Hence, the second part is also proved.

